Problem #91: Counting Filled Tic-Tac-Toe Boards

[Jameson]

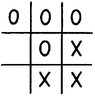
A standard tic-tac-toe board (or noughts and crosses) is a 3x3 grid, with 9 total spaces.

View attachment 1796
There are many different ways that the X's and O's can be placed on the board. If we ignore for now the rule that 3 pieces of one type in a row wins, how many ways can we fill the board completely? Assume that the same piece, X or O, plays first each time so you will always have 1 more of that piece than the other.

Note: The problem isn't to count moves that lead to a certain position. 1 filled board can be reached many ways. Just count the number of total filled boards. Also, don't worry about rotations or reflections for you guys who are more advanced.
--------------------

 

[Jameson]

Congratulations to the following members for their correct solutions:

1) MarkFL

Solution (from MarkFL):

Spoiler

This problem boils down to looking at how many ways to choose 9 things 5 at a time, or equivalently, how to choose 9 things 4 at a time. Thus, the number $N$ of distinct filled boards is given by:

$$N={9 \choose 5}={9 \choose 4}=\frac{9!}{4!\cdot5!}=\frac{9\cdot8\cdot7\cdot6}{4\cdot3\cdot2}=9\cdot7\cdot2=14(10-1)=140-14=126$$

Thus, we find there are 126 distinct filled boards.