Problem Of The Week #503 June 24th 2022

[anemone]

Here is this week's POTW:

-----

Let $x$ and $y$ be the positive real numbers such that $x^5+y^3 \le x^2+y^2$.

Prove that $x(x+y)\le 2$.

-----

 

[anuttarasammyak]

This is not an answer but an observation of the relevant graphs for what is going on. I observe a funny shape.

 

[Steve4Physics]

This is not an answer but an observation of the relevant graphs for what is going on. I observe a funny shape.
View attachment 313738

Yes, I was playing around with this and also saw the same. To expand a bit...

$x^5 +y^3 \le x^2 + y^2$ with $x, y>0$ defines a region in the 1st quadrant of the xy plane as shown below:

Call this region, shaded red, $R_1$. Call the red boundary-line (corresponding to the equality condition) $B_1$.

Similarly $x(x+y) \le 2$ defines region $R_2$ with boundary-line $B_2$ (blue).

Overlaying these gives:

(If anyone wants to set-up/play with these graphs, see
https://www.desmos.com/calculator/og3edz9st5)

The problem stated is equivalent to showing that $R_2$ completely contains $R_1$; i.e. that every point (x, y) in $R_1$ is also in $R_2$.

(The converse is not necessarily true: there are points in $R_2$ that are not in $R_1$.)

It is easy to determine that$B_1$ passes through (0,1), (1,0) and (1,1) and that $B_2$ passes through (1,1) and (√2,1).

Note that (1,1) is a common point and we can show $B_1$ and $B_2$ just touch here – i.e. they have a common tangent – as follows:

For $B_1:x^5 +y^3 - x^2 - y^2=0$
Differentiating implicitly gives:
$\frac {dy}{dx} = \frac {x(2- 5x^3)}{y(3y– 2}$
At (1,1) $\frac {dy}{dx} = \frac {1(2-5*1)^3}{1(3*1-2)} = -3$

For $B_2: x(x+y) =2$
Differentiating implicitly gives:
$\frac {dy}{dx} = -\frac {2x+y}{x}$
At (1,1), $\frac {dy}{dx}= -\frac{2*1+1}{1} = -3$ the same as for $B_1$.

We also note that at (1,1) $B_1$ is concave upwards and $B_2$ is concave downwards. From visual inspection $R_2$ entirely contains $R_1$, as required. But that's no proof.

 

[anuttarasammyak]

( cont. of my post #2 )
Let us name
Graph 1 : $x^5-x^2+y^3-y^2=0$
Graph 2 : $x(x+y)=2$
The x coordinate of the crossing point satisfies
$$(x-1)(x^7+x^6-x^4+6x^3+6x^2-8x-8)=0$$
So we now (x,y)=(1,1) is a crossing point, let us say it P.
At P by simple calculation
the gradient of graph 1 = the gradient of graph 2 = -3
The second derivative of graph 1 = 4
The second derivative of graph 2 = -54
So we show the graph 2 surpass graph 1 around point P.
This is just a local discussion around P.

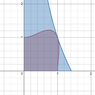
The graph of the remaining part of the above crossing point equation

So as for x < 1.083... where the red dot point in the graph, we shall not have another crossing which goes with the statement.
The red point should not correspond to another crossing but the x bounded point, but I would like to get a confirmation about my interpretation.
Anyway, the above three lines I said watching the graph are not proof but a speculation.

For graph 1
$$\frac{dy}{dx}=-\frac{x(5x^3-2)}{y(3y-2)}$$
dy/dx=0 at x=0, $(\frac{2}{5})^{1/3}$, i.e. (0,1), $((\frac{2}{5})^{1/3},\beta)$
where $\beta^3+\beta^2+(2/5)^{5/3}+(2/5)^{2/3},\beta>0$
dx/dy=0 at y=0, 2/3, i.e. $(1,0),(\alpha,2/3)$ where
$\alpha^5-\alpha^2-4/27=0,\alpha>0$

For graph 2
$$\frac{dy}{dx}=\frac{\frac{x}{\sqrt{x^2+4}}-1}{2} <0$$
So y is monotonously decreasing function of x
for x=0, y=$+\infty$ >1
for x=$(\frac{2}{5})^{1/3}, y=\frac{\sqrt{(2/5)^{2/3}+4}-(2/5)^{1/3}}{2}$ > $\beta$ by numerical calculation
for y=0, x=$\sqrt{2}$ > 1
for y=2/3, x=$\frac{2\sqrt{19}-1}{3} > \alpha$ by numerical calculation

That means graph 2 surpass graph 1 in region x,y>0.

Thus I wish the statement was proved, though I would like to know a more elegant solution very much.

 

[Steve4Physics]

( cont. of my post #2 )
Let us name
Graph 1 : $x^5-x^2+y^3-y^2=0$
Graph 2 : $x(x+y)=2$
The x coordinate of the crossing point satisfies
$$(x-1)(x^7+x^6-x^4+6x^3+6x^2-8x-8)=0$$
So we now (x,y)=(1,1) is the crossing point, let us say it P.
At P by simple calculation
the gradient of graph 1 = the gradient of graph 2 = -3
The second derivative of graph 1 = 4
The second derivative of graph 2 = -54
So we show the graph 2 surpass graph 1 around point P.
This is just local discussion around P.

Working out the second derivatives (by hand) was too daunting for me!

It's worth noting that the maximum value of x and the maximum vaue of y in the region of interest (1st quadrant) can easily be found by considering $\frac {dy}{dx} = 0$ and $\frac {dy}{dx} = ∞$. This can support the visual argument.

However, I presume a rigorous analytical proof is required so I'm stuck.

 

[Steve4Physics]

I wish the statement was proved, though I would like to know a more elegant solution very much.

Me too!

 

[anuttarasammyak]

(Post script to my post #4)
We can make similar problems, e.g.,
------------
For positive real numbers x and y
$$x^5-x^2+y^3-y \leq 0$$
satisfy
$$y<x^{-3/2}$$
and
$$\sqrt{x}+xy<2$$
--------------

 

[bob012345]

Thus I wish the statement was proved, though I would like to know a more elegant solution very much.

I found what I think is at least a simple solution;

Given $$x^5+y^3 \le x^2+y^2$$ is valid in some domain $R_1$ we have $$ 0 \le x^2+y^2 - x^5 - y^3$$ we can add the same thing to both sides without changing the inequality, in this case the quantity $x^2 + xy$;

$$ x^2 + xy \le 2x^2+y^2 - x^5 - y^3 + xy$$ where the RHS has a maximum of 2 for all $x,y>0$ at $(1,1)$ thus

$$x(x + y) \le 2$$ for all $(x,y)$ in $R_1$

 

[Steve4Physics]

$$ x^2 + xy \le 2x^2+y^2 - x^5 - y^3 + xy$$ where the RHS has a maximum of 2 for all $x,y>0$ at $(1,1)$ thus

Nice. But may I ask how you determined that the RHS has a maximum at (1,1) and that this is the only maximum (for x,y>0)?

(I'm probably being a bit slow but I just can't see how to establish that without some calculus.)

 

[bob012345]

Nice. But may I ask how you determined that the RHS has a maximum at (1,1) and that this is the only maximum (for x,y>0)?

(I'm probably being a bit slow but I just can't see how to establish that without some calculus.)

Thanks. I left that part out for brevity but here is the calculus;

Take the partial derivatives of the function on the RHS $$\frac{\partial f(x,y)}{\partial x} = 4x + y -5x^4 = 0$$ and $$\frac{\partial f(x,y)}{\partial y} = x +2y -3y^2 = 0$$ these yield;

$$y = 5x^4 -4x$$ and $$x = 3y^2 -2y$$ substituting we get;

$$x = 75x^8 -120x^5 -10x^4 + 48x^2 +8x$$ or $$75x^7 -120x^4 -10x^3 + 48x +7 = 0$$

We can test if $x=1$ works and it does. Wolfram Alpha gives another real solution of $x≈0.90173$ but that yields a negative $y$ value and is also a relative minimum so is rejected since we are only concerned with positive $(x,y)$ so $x=1$ yields $y=1$ and we test those
$$f(1,1) = 2x^2 + xy +y^2 - x^5 - y^3 = 2 + 1 + 1 - 1 -1 = 2$$

Here is a plot of the function and the $z=2$ plane and point $(1,1,2)$ for reference.

https://www.math3d.org/oEvyPVWTx

 

[Steve4Physics]

Thanks. I left that part out for brevity but here is the calculus;

Thanks for taking the time to do that. I thought there might be some non-calculus approach I was missing.

$$75x^7 -120x^4 -10x^3 + 48x +7 = 0$$We can test if $x=1$ works and it does. Wolfram Alpha gives another real solution of $x≈0.90173$ but that yields a negative $y$ value and is also a relative minimum so is rejected since we are only concerned with positive $(x,y)$ so $x=1$ yields $y=1$

The problem (for me) is that this means we are having to use software such as Wolfram Alpha. Otherwise we can't easily demomstrate that (1,1) is the only maximum. For example, there could be a local maximum of (say) 3 at some point in the domain $R_1$. Ideally, it would be nice to have a software-free approach to eliminate such possibilities.

Edit: minor change/typo's.

 

[bob012345]

Thanks for taking the time to do that. I thought there might be some non-calculus approach I was missing.


The problem (for me) is that this means we are having to use software such as Wolfram Alpha. Otherwise we can't easily demonstrate that (1,1) is the only maximum. For example, there could be a local maximum of (say) 3 at some point in the domain $R_1$. Ideally, it would be nice to have a software-free approach to eliminate such possibilities.

Edit: minor change/typo's.

Thinking about this a little more I think we can demonstrate there is only one relevant maximum by thinking about the form of the derivatives which are used to find the maxima of the function on the RHS above;

$$x = 3y^2 -2y$$ and
$$y = 5x^4 -4x$$

From these we can deduce the following;

The first is a parabola opening to the right or positive x-axis symmetrical around the line $y=\frac{1}{3}$, the vertex is at $(-\frac{1}{3}, \frac{1}{3})$ which intersects the y-axis at $(0,0)$ and $(0,\frac{2}{3})$ and it is monotonically increasing in the first quadrant for $x>0$ and $y>\frac{2}{3}$,

The second is a quartic which opens towards positive $y$, has a vertex in the fourth quadrant and has two roots one at $(0,0)$ and the other at $(\sqrt[3]{\frac{4}{5}}, 0)$ and is monotonically increasing for $x>\sqrt[3]{\frac{4}{5}}$ and $y>0$.

There can be only one intersection of these two monotonically increasing functions in the positive quadrant which must then be at the point previously identified at $(1,1)$. Thus this is the only maximum of the function in the positive quadrant and is equal to 2.

Though we did not require it, visually, it looks like this;

You made me use my brain a little more @Steve4Physics , thanks!