Problem of the week #98 - February 10th, 2014

[anemone]

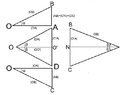
Two similar vertical posts AB and DC stand with A and D on the ground. O is a point on the ground such that the angles of elevation of B and C from O are both $\alpha$. Given that $\angle AOD=2\beta$ and N is the midpoint of BC.

a. If $\angle BOC=2\theta$, show that $\sin \theta=\cos \alpha \sin \beta$.
b. If the angle of elevation of N from O is $\phi$, show that $\tan \phi =\tan \alpha \sec \beta$.

--------------------
Remember to read the http://www.mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to http://www.mathhelpboards.com/forms.php?do=form&fid=2!

 

[anemone]

Congratulations to lfdahl for his correct solution.

Solution from lfdahl:

Spoiler

With reference to the attached figure:

View attachment 1992
[TABLE="class: grid, width: 1000"]
[TR]
[TD]a. \[cos(\alpha)=\frac{|OA|}{|OB|}\;\;\;\;sin(\beta)= \frac{|O'A|}{|OA|} \\\\ sin(\theta )=\frac{|O'A|}{|OB|}=\frac{|OA|}{|OB|}\frac{|O'A|}{|OA|}=cos(\alpha)sin(\beta)\]

\[tan(\alpha)=\frac{|AB|}{|OA|}\;\;\;\;cos(\beta)= \frac{|OO'|}{|OA|} \\\\\\ tan(\phi )=\frac{|AB|}{|OO'|}=\frac{\frac{|AB|}{|OA|}}{ \frac{|OO'|}{|OA|} }=tan(\alpha)(cos(\beta))^{-1}=tan(\alpha)sec(\beta)\] [/TD]
[TD]b. \[cos(\alpha)=\frac{|OA|}{|OB|}\;\;\;\;sin(\beta)= \frac{|O'A|}{|OA|} \\\\ sin(\theta )=\frac{|O'A|}{|OB|}=\frac{|OA|}{|OB|}\frac{|O'A|}{|OA|}=cos(\alpha)sin(\beta)\]\[tan(\alpha)=\frac{|AB|}{|OA|}\;\;\;\;cos(\beta)= \frac{|OO'|}{|OA|} \\\\\\ tan(\varphi )=\frac{|AB|}{|OO'|}=\frac{\frac{|AB|}{|OA|}}{ \frac{|OO'|}{|OA|} }=tan(\alpha)(cos(\beta))^{-1}=tan(\alpha)sec(\beta)\][/TD]
[/TR]
[/TABLE]