I Problem with checking solution by wolframalpha

[polibuda]

TL;DR Summary

System of differential equations

My problem is that I can't check solution of task in any calculator (only in wolfram). I have the system of differential equations:
x'=3x-4y+1
y'=4x-7y+10t
I solved it and the result is:

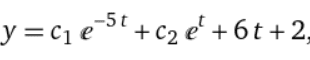
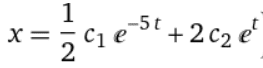
but when I check result in wolfram I receive something like that:

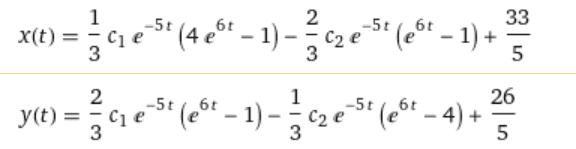
What is the problem? Are any else another calculators to check solutions of system of differential equations?

 

[jedishrfu]

Have you hand checked your result? ie compute x' and y' from your solution and plug back into the original to verify that they work?

I would not waste time unless you've got it to waste on why an online calculator seems to differ from your result.

 

[polibuda]

That is good advice. Thank you for help.

 

[phyzguy]

Are you sure you typed it correctly into Wolfram Alpha? The solution you posted can't be right, because there is no way for it to give the 10t term on the RHS of the y' equation.

 

[Infrared]

Are you sure you typed it correctly into Wolfram Alpha? The solution you posted can't be right, because there is no way for it to give the 10t term on the RHS of the y' equation.

In particular, it looks like the WA answer solves the system

$$x'=3x-4y+1$$ $$y'=4x-7y+10$$

(with a constant $10$ instead of $10t$). I think this is the typo.