Problems solving this differential equation for a Pendulum with Mathematica

[Lambda96]

TL;DR

Mathematica does not solve the differential equations

Hi,

unfortunately, I have problems that Mathematica does not solve the differential equation. The task is as follows and it is about the task c

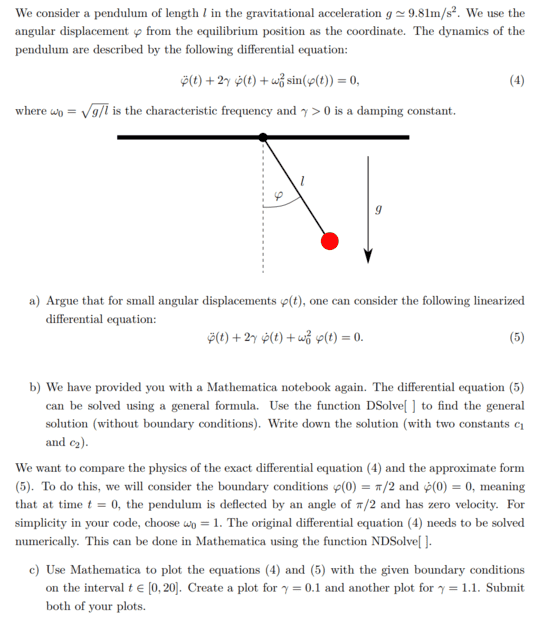
In the Mathematica Notebook, the following was written for task c

"You can use the following two lines of code to produce the solutions of the exact and approximated differential equations with boundary conditions. After that, write a plot[ ] function to sketch the two together."

exact[t_] := Evaluate[phi[t] /. NDSolve[..., phi[t], {t, 0, 20}]];
approx[t_] := Evaluate[phi[t] /. DSolve[..., phi[t], t]];I then tried to calculate the differential equation for equation (4) using the two codes and got the following

I then tried solving the differential equation using only NDSolve and get the following.

I am a beginner in Mathematica, so I do not know what I have done wrong in the two formulas?

 

[Dale]

As the error messages say, your initial conditions are wrong. You have

phi[0]==0

and

phi[0]==Pi/2

which is not meaningful. You should have the first derivative of phi for one of those.

phi'[0]==...

 

[Lambda96]

Thanks Dale for your help and for looking over my code

I have now tried plotting the differential equations again, but this time with phi'[0]=0 and with $\gamma=0.1$ and got the following.

Is there any way that I can show in the plot which function is which?

 

[DrClaude]

Is there any way that I can show in the plot which function is which?

There are different options. Try for instance

Plot[{exact[t],approx[t]},{t,0,20},PlotLegends->"Expressions"]

 

[Lambda96]

Thanks DrClaude for your help, this is exactly what I was looking for