Anakin Skywalker
- 1
- 0
Hello.
Given a range of time in which an event can occur an indefinite number of times, we say a random variable X folows a poisson distribution when it follows this statements:
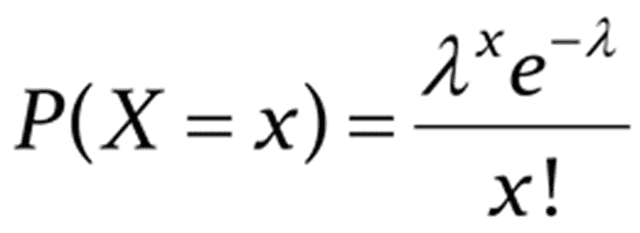
I would like to know how this expression is deduced.
P.S.: I used the informations in the wikipedia's page, so I'm not so sure that these topics are right.
https://en.wikipedia.org/wiki/Poiss..._Poisson_distribution_an_appropriate_model.3F
Given a range of time in which an event can occur an indefinite number of times, we say a random variable X folows a poisson distribution when it follows this statements:
- X is the number of times an event occurs in an interval and X can take values 0, 1, 2, …
- The occurrence of one event does not affect the probability that a second event will occur. That is, events occur independently.
- The rate at which events occur is constant. The rate cannot be higher in some intervals and lower in other intervals.
- Two events cannot occur at exactly the same instant.
- The probability of an event in an interval is proportional to the length of the interval.
I would like to know how this expression is deduced.
P.S.: I used the informations in the wikipedia's page, so I'm not so sure that these topics are right.
https://en.wikipedia.org/wiki/Poiss..._Poisson_distribution_an_appropriate_model.3F