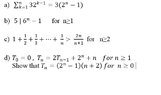Discussion Overview
The discussion revolves around solving discrete mathematics problems using mathematical induction. Participants are seeking assistance with specific problems and the methodology of induction proofs.
Discussion Character
- Homework-related
- Mathematical reasoning
Main Points Raised
- One participant requests help with discrete math problems, specifically asking for proofs using induction.
- Another participant suggests a specific formula involving a summation and proposes that the first step is to verify the base case for n=1.
- A later reply confirms that the base case is true for n=1 and indicates that the problems are practice questions for an exam, asking for hints on how to proceed with the last problem.
- Further advice is given to state the induction hypothesis and suggests that using the recursion will be important for the induction step.
Areas of Agreement / Disagreement
Participants generally agree on the steps involved in proving the problem using induction, but the specific problems and methods remain unresolved as participants are still in the process of working through them.
Contextual Notes
There is a mention of a recursion that needs to be expressed in terms of n+1, but the details of this recursion are not fully elaborated, leaving some assumptions and steps unspecified.