SimpliciusH
- 32
- 0
I apologize if I'm posting this in the wrong subforum, I wasn't quite sure where statistics and distribution questions should go. I have major problems understanding the concepts involved with this kind of stuff.
On a country road an average of 30 cars pass per hour. Four hitch-hikers are standing near a sign and waiting for a lift. Supposing each driver is glad to take exactly one hitch-hiker, what is the probability that all the hitch-hikers will have found someone to take them to their destination after 10 minutes?
Poisson distribution
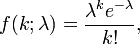
I'm not quite sure how to approach this. At first glance this seems to be a Poisson distribution since I'm searching for the probability of 4 cars passing by in 10 minutes, and any particular car passing by doesn't seem to (in my opinion) change the probability of any other car passing by.
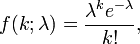
So I took k=4, since I was interested in four cars passing by and I took lambda as 5, I got a probability of 0.17546 (17.5%), which intuitively seems a bit low considering lambda.
Is this naive approach correct or am I missing something?
Thanks for the help!
Edit:
A second after posting I realized that I've only calculated the probability for exactly four cars passing by, but the set conditions are also fulfilled if any number of cars greater than 4 pass by in those 10 minutes. How can I account for this?
Homework Statement
On a country road an average of 30 cars pass per hour. Four hitch-hikers are standing near a sign and waiting for a lift. Supposing each driver is glad to take exactly one hitch-hiker, what is the probability that all the hitch-hikers will have found someone to take them to their destination after 10 minutes?
Homework Equations
Poisson distribution
The Attempt at a Solution
I'm not quite sure how to approach this. At first glance this seems to be a Poisson distribution since I'm searching for the probability of 4 cars passing by in 10 minutes, and any particular car passing by doesn't seem to (in my opinion) change the probability of any other car passing by.
So I took k=4, since I was interested in four cars passing by and I took lambda as 5, I got a probability of 0.17546 (17.5%), which intuitively seems a bit low considering lambda.
Is this naive approach correct or am I missing something?
Thanks for the help!
Edit:
A second after posting I realized that I've only calculated the probability for exactly four cars passing by, but the set conditions are also fulfilled if any number of cars greater than 4 pass by in those 10 minutes. How can I account for this?