SUMMARY
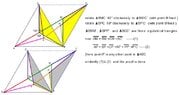
The discussion centers on proving the inequality $PA + PB + PC \geq MA + MB + MC$ within an acute triangle ABC, where M is an inner point and the angles $\angle AMB$, $\angle BMC$, and $\angle CMA$ each measure 120 degrees. The participants explore geometric properties and relationships that arise from the configuration of points A, B, C, and M. The conclusion emphasizes the necessity of understanding the implications of angle measures and point placements in proving the stated inequality.
PREREQUISITES
- Understanding of triangle geometry, specifically acute triangles.
- Familiarity with geometric inequalities and their proofs.
- Knowledge of angle relationships in polygons, particularly the properties of angles summing to 360 degrees.
- Basic skills in constructing geometric proofs and reasoning.
NEXT STEPS
- Research geometric inequalities related to points within triangles.
- Study the properties of angles in polygons, focusing on configurations involving 120-degree angles.
- Explore advanced triangle centers and their implications on geometric inequalities.
- Learn about the use of vector methods in proving inequalities in geometry.
USEFUL FOR
Mathematicians, geometry enthusiasts, and students studying advanced triangle properties and inequalities will benefit from this discussion.