Quine-McCluskey method: Prime implicants - disjunctive minimal forms

[mathmari]

Hey!

I am looking at the following:
Use the Quine-McCluskey method to determine the respective prime implicants for the following boolean functions and find a disjunctive minimal form. If available, also give all others disjunctive minimal forms.

\begin{equation*}f(x_1, x_2, x_3, x_4)=\bar{x}_1x_2(\bar{x}_3\lor x_3\bar{x}_4)\lor x_1(x_3\bar{x}_4\lor x_2)\lor (x_1\bar{x}_2\lor x_2)x_3\lor \bar{x}_1x_2(\bar{x}_3x_4\lor \bar{x}_3\bar{x}_4\lor x_3x_4)\end{equation*}

First, we open the parentheses:
\begin{equation*}f(x_1, x_2, x_3, x_4)=\bar{x}_1x_2\bar{x}_3\lor \bar{x}_1x_2x_3\bar{x}_4\lor x_1x_3\bar{x}_4\lor x_1x_2\lor x_1\bar{x}_2x_3\lor x_2x_3\lor \bar{x}_1x_2\bar{x}_3x_4\lor \bar{x}_1x_2\bar{x}_3\bar{x}_4\lor \bar{x}_1x_2x_3x_4\end{equation*}

If one variable doesn't appear at one term it is replaced by $x_i \lor \bar{x}_i$. So we get
\begin{align*}f(x_1, x_2, x_3, x_4)&=\bar{x}_1x_2\bar{x}_3(x_4\lor \bar{x}_4)\lor \bar{x}_1x_2x_3\bar{x}_4\lor x_1(x_2\lor \bar{x}_2)x_3\bar{x}_4\lor x_1x_2(x_3\lor \bar{x}_3)(x_4\lor \bar{x}_4)\lor x_1\bar{x}_2x_3(x_4\lor \bar{x}_4) \\ & \lor (x_1\lor \bar{x}_1)x_2x_3(x_4\lor \bar{x}_4)\lor \bar{x}_1x_2\bar{x}_3x_4 \lor \bar{x}_1x_2\bar{x}_3\bar{x}_4\lor \bar{x}_1x_2x_3x_4\end{align*}

We simplify that expression:
\begin{align*}f(x_1, x_2, x_3, x_4)&=\bar{x}_1x_2\bar{x}_3x_4\lor \bar{x}_1x_2\bar{x}_3\bar{x}_4\lor \bar{x}_1x_2x_3\bar{x}_4\lor x_1x_2x_3\bar{x}_4\lor x_1\bar{x}_2x_3\bar{x}_4\lor x_1x_2x_3x_4\lor x_1x_2\bar{x}_3x_4\\ & \lor x_1x_2x_3\bar{x}_4\lor x_1x_2\bar{x}_3x_4\lor x_1\bar{x}_2x_3x_4 \lor x_1\bar{x}_2x_3\bar{x}_4\lor x_1x_2x_3x_4\lor x_1x_2x_3\bar{x}_4 \\ & \lor \bar{x}_1x_2x_3x_4\lor \bar{x}_1x_2x_3\bar{x}_4\lor \bar{x}_1x_2\bar{x}_3x_4 \lor \bar{x}_1x_2\bar{x}_3x_4\lor \bar{x}_1x_2x_3x_4\end{align*}

Some terms appear more than once, so we can write these once and so we get:
\begin{align*}f(x_1, x_2, x_3, x_4)&=\bar{x}_1x_2\bar{x}_3x_4\lor \bar{x}_1x_2\bar{x}_3\bar{x}_4\lor \bar{x}_1x_2x_3\bar{x}_4\lor x_1x_2x_3\bar{x}_4\lor x_1\bar{x}_2x_3\bar{x}_4\lor x_1x_2x_3x_4\lor x_1x_2\bar{x}_3x_4 \\ & \lor x_1\bar{x}_2x_3x_4\lor \bar{x}_1x_2x_3x_4\end{align*}

It holds that $x^0=\bar{x}$ and $x^1=x$. So we can write the expression in the following form:
\begin{align*}f(x_1, x_2, x_3, x_4)&=x_1^0x_2^1x_3^0x_4^1\lor x_1^0x_2^1x_3^0x_4^0\lor x_1^0x_2^1x_3^1x_4^0\lor x_1^1x_2^1x_3^1x_4^0\lor x_1^1x_2^0x_3^1x_4^0\lor x_1^1x_2^1x_3^1x_4^1\lor x_1^1x_2^1x_3^0x_4^1 \\ & \lor x_1^1x_2^0x_3^1x_4^1\lor x_1^0x_2^1x_3^1x_4^1\end{align*}

We calculate the weight of each term:
\begin{align*}&g(x_1^0x_2^1x_3^0x_4^1)=2 \\ &g( x_1^0x_2^1x_3^0x_4^0)=1 \\ & g( x_1^0x_2^1x_3^1x_4^0)=2 \\ & g( x_1^1x_2^1x_3^1x_4^0)=3 \\ & g( x_1^1x_2^0x_3^1x_4^0)=2 \\ & g( x_1^1x_2^1x_3^1x_4^1)=4 \\ & g( x_1^1x_2^1x_3^0x_4^1)=3 \\ & g( x_1^1x_2^0x_3^1x_4^1)=3 \\ & g( x_1^0x_2^1x_3^1x_4^1)=3\end{align*}

We create the following table:
View attachment 8988

Two terms $m$ and $m'$ can be combined when $|g(m)-g(m')| = 1$. That means that we have to compare all terms of two neighboring classes if they differ by one negation.

We get the following:
View attachment 8989

We can combine two rows if they have "-" on the same position.

View attachment 8990

No more combinations can be done.

So we have the four prime terms:
\begin{align*}p_1=m_1+m_2+m_3+m_8=x_1^0x_2^1=\bar{x}_1x_2 \\ p_2=m_2+m_6+m_8+m_9=x_2^1x_4^1=x_2x_4 \\ p_3=m_3+m_5+m_8+m_9=x_2^1x_3^1=x_2x_3 \\ p_4=m_4+m_5+m_7+m_9=x_1^1x_3^1=x_1x_3\end{align*}

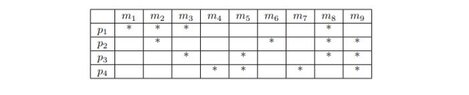
The table of prime terms is:
View attachment 8991

The columns are pairwise compared to whether there is not a column in which the marked primer terms are a subset of the marked primer terms of the other column. If this is the case, then the superset column can be deleted because all conjunctions must be detected, and therefore the conjunction with the superset is also included by selecting the conjunction with the subset.

We can delete the columns $m_2, m_3, m_8$ due to the column $m_1$. We can delete also the columns $m_5, m_7, m_9$ due to the column $m_4$.

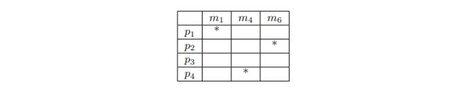
Then the table looks as follows:
View attachment 8992

Now we compare the rows (prime terms) of the table in pairs, if there is not one row in which the marked minterms are a subset of the marked minterms of the other row. If this is the case, then the primerm with the subset can be deleted, because one can take the other primerm as a substitute for each marking of the primed primer. The relation is exactly the opposite here as with the columns.

We delete the (empty) row $p_3$ and so we get
View attachment 8993 Therefore we have the prime terms $p_1, p_2, p_4$.

Now the selected prime terms have to be linked to the solution equation by disjunction:
\begin{equation*}p_1\lor p_2\lor p_4=\bar{x}_1x_2\lor x_2x_4\lor x_1x_3\end{equation*}
Is everything correct? (Wondering)

 

[I like Serena]

I am looking at the following:
Use the Quine-McCluskey method to determine the respective prime implicants for the following boolean functions and find a disjunctive minimal form. If available, also give all others disjunctive minimal forms.

\begin{equation*}f(x_1, x_2, x_3, x_4)=\bar{x}_1x_2(\bar{x}_3\lor x_3\bar{x}_4)\lor x_1(x_3\bar{x}_4\lor x_2)\lor (x_1\bar{x}_2\lor x_2)x_3\lor \bar{x}_1x_2(\bar{x}_3x_4\lor \bar{x}_3\bar{x}_4\lor x_3x_4)\end{equation*}

First, we open the parentheses:
\begin{equation*}f(x_1, x_2, x_3, x_4)=\bar{x}_1x_2\bar{x}_3\lor \bar{x}_1x_2x_3\bar{x}_4\lor x_1x_3\bar{x}_4\lor x_1x_2\lor x_1\bar{x}_2x_3\lor x_2x_3\lor \bar{x}_1x_2\bar{x}_3x_4\lor \bar{x}_1x_2\bar{x}_3\bar{x}_4\lor \bar{x}_1x_2x_3x_4\end{equation*}
...
Now the selected prime terms have to be linked to the solution equation by disjunction:
\begin{equation*}p_1\lor p_2\lor p_4=\bar{x}_1x_2\lor x_2x_4\lor x_1x_3\end{equation*}

Hey mathmari!

I'm not familiar with the Quine-McCluskey method.
Instead I verified your result by drawing a Karnaugh Diagram.
View attachment 9001
It seems to me that the expression should be different. (Worried)

Shouldn't the prime expression be:
$$x_2\lor x_1x_3 $$
(Wondering)

 

[mathmari]

I'm not familiar with the Quine-McCluskey method.
Instead I verified your result by drawing a Karnaugh Diagram.

It seems to me that the expression should be different. (Worried)

Shouldn't the prime expression be:
$$x_2\lor x_1x_3 $$
(Wondering)

So, is there a unique solution? (Wondering)

 

[I like Serena]

So, is there a unique solution?

Looking at the Karnaugh Diagram for this case, I believe this is the only solution that is this simple.
That is, if we pick a different covering, then we can remove symbols while still having the same cover.
If I understand correctly, that means that it is indeed the only prime implicant. (Thinking)