Ratio of areas of squares - Challenging problem

[Lancelot1]

Hello all,

I have encountered a very difficult question in geometry. The question has several parts. I really need your help. I have tried solving the first and second ones, not sure I did it correctly, and certainly don't know how to proceed and what the results means. I would really appreciate your help in solving this tricky one...My solution is at the end, below the question.

Thank you in advance !

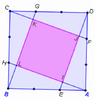
1) A square ABCD is given. Each vertex is connected with a point on the opposite edge (clockwise) such that the ratio between the closer part to the vertex and the edge of the square is 1:3. Find the ratio of areas between the squares KLIJ and ABCD.

View attachment 8006

2) Solve the previous problem when the ratio is 1:4 instead of 1:3.

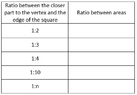
3) Complete the following table:

View attachment 8005

What is your conclusion ?

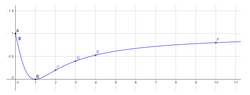
4) Look at the graph of

\[f(x)=\frac{(x-1)^{2}}{x^{2}+1}\]

View attachment 8007

What is the geometric explanation to the function's behavior ?
What is the meaning of area where the function increases / decreases ? What is the meaning of the asymptote ? Can this function be generalized to the negative region ? What does it mean ?

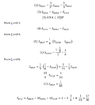
My solution (assuming the length is 1):

View attachment 8008

View attachment 8009

 

[Opalg]

This is an interesting problem. I found it easier to take the size of the large square $ABCD$ to be $n\times n$, so that the lengths of the segments $AE$, $BH$, ... , are $1$.

I think that the best way to tackle the problem is to use similar triangles. The triangles $ABH$ and $AIE$ are similar (having the same angles). The sides of the larger triangle $ABH$ are $1$, $n$ and (by Pythagoras) $\sqrt{n^2+1}$. The hypotenuse of the smaller triangle $AIE$ is $1$, so the ratio of corresponding sides in the triangles is $1:\sqrt{n^2+1}$. From that, you can find the lengths of the other two sides of the smaller triangle.

Now look at the line $AH = AI + IL + LH$. In that equation, you now know everything except $IL$. So you can use that to find the length of the sides of the inner square $IJKL$, which turns out to be $\dfrac{n(n-1)}{\sqrt{n^2+1}}.$ That gives the ratio of the areas of the squares $ABCD$ and $IJKL$ to be $\dfrac{(n-1)^2}{n^2+1}$.

Your calculation using areas is also a good method, and it is correct right up to the last line $S_{KLIJ} = S_{ABCD} - 3S_{\triangle DEA} + 4S_{\triangle DJF}$, which should be $S_{KLIJ} = S_{ABCD} - 4S_{\triangle DEA} + 4S_{\triangle DJF}$.