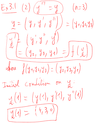nacho-man
- 166
- 0
Could someone please provide a worked solution for me. I think that is the only way I will understand this. It was covered very vaguely in our lectures and my notes start talking about vectors and using co-domain notation which is very frustrating!
1. $y''(x) = x + y'(x) + e^{y(x)}$ with $y(0)=0, y'(0)=1$I know MHB doesn't endorse just handing out solutions, so I will try and attempt the second problem myself if someone may help me with the first. I really need to learn this for my exam in 7 days.
2. $y'''(x) = y(x)$ with $y(1) = 4, y'(1)=4, y''(1)=0$
1. $y''(x) = x + y'(x) + e^{y(x)}$ with $y(0)=0, y'(0)=1$I know MHB doesn't endorse just handing out solutions, so I will try and attempt the second problem myself if someone may help me with the first. I really need to learn this for my exam in 7 days.
2. $y'''(x) = y(x)$ with $y(1) = 4, y'(1)=4, y''(1)=0$