rasofia77
- 22
- 0
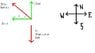
While traveling on a train, two boys play catch in the aisle. The train is moving north at 30.0 m/s. The ball is tossed front to back at 5.0 m/s relative to the boys. A bystander on the highway observes the ball being tossed toward the back. To the bystander, what is the relative speed of the ball?
So, I am currently very, very confused in physics. (By the way there's that equation of oVe=oVm+mVe)
I simply don't understand motion or relative motion or most of the things that come out of my physics teacher's mouth. Okay, so for this answer all I would say is 30-5 just because the ball goes south and the train goes north, so 25? But I don't understand, really, how to put that in terms of the equation or even if it's right. And if it were, what would go with the final answer direction-wise? South, North..? Because obviously the ball is going south...but the train is faster and going north so would it be north as the final answer (from the bystander's point of view?)
So, I am currently very, very confused in physics. (By the way there's that equation of oVe=oVm+mVe)
I simply don't understand motion or relative motion or most of the things that come out of my physics teacher's mouth. Okay, so for this answer all I would say is 30-5 just because the ball goes south and the train goes north, so 25? But I don't understand, really, how to put that in terms of the equation or even if it's right. And if it were, what would go with the final answer direction-wise? South, North..? Because obviously the ball is going south...but the train is faster and going north so would it be north as the final answer (from the bystander's point of view?)