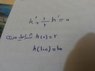MATLAB Runge Kutta Method: Solve Example with MATLAB

Click For Summary
SUMMARY

The discussion focuses on solving a boundary value problem using the Runge Kutta method in MATLAB. The equation in question is h'' + (1/r)h' = 0, where r is treated as a constant. The solution involves integrating the equation to obtain h' + (1/r)h = C, leading to the general solution h(x) = C2 + C·x + C1e^(-x/r). Participants emphasize the importance of determining the constants to fit specific constraints and suggest converting the boundary value problem into an initial value problem (IVP) for easier simulation.

PREREQUISITES
  • Understanding of the Runge Kutta method for numerical solutions
  • Familiarity with MATLAB programming and simulation
  • Knowledge of boundary value problems and initial value problems
  • Basic calculus, particularly integration techniques
NEXT STEPS
  • Explore MATLAB's ODE solvers for implementing the Runge Kutta method
  • Study boundary value problem techniques, specifically the shooting method
  • Learn about converting boundary value problems to initial value problems
  • Investigate numerical integration methods in MATLAB for solving differential equations
USEFUL FOR

Students and professionals in engineering, applied mathematics, and computational science who are working on numerical simulations of differential equations using MATLAB.

num3n
Messages
1
Reaction score
0
hello all dear

please help me
can solve this Example By Simulation With matlab
 

Attachments

  • 45978de1ada5246b1621b793caa1c02bf386de6e798f2d726652136470493a69.jpg
    45978de1ada5246b1621b793caa1c02bf386de6e798f2d726652136470493a69.jpg
    25.9 KB · Views: 501
num3n said:
can solve this Example By Simulation With matlab
I am not quite sure of your parameters. As far as I can make out your equation is h''+\frac{1}{r}h'=0. Now I wonder: Is r a constant? If so, just integrate and get h'+\frac{1}{r}h=C (C is a constant) and from there h(x) = C_{2}+C\cdot x + C_{1}e^{\frac{-x}{r}}. Nom determine the constants to fit your constraints.
 

Similar threads

MATLAB Problem with Runge-Kutta script file
  • · Replies 4 ·
Replies
4
Views
2K
MATLAB Solving an Elastic Pendulum Equation with Matlab/Excel
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Solving 3D TDSE with Runge-Kutta Method
  • · Replies 3 ·
Replies
3
Views
3K
Undergrad Runge-Kutta 4 w/ some sugar on the top: How to do error approximation?
  • · Replies 65 ·
3
Replies
65
Views
8K
MATLAB Find Scilab & MATLAB Help Forums | Converting Code & Programming Questions
  • · Replies 6 ·
Replies
6
Views
4K
MATLAB Using 2 MATLAB files to simulate 3 plots
  • · Replies 1 ·
Replies
1
Views
2K
MATLAB Help converting MATLAB to Scilab code
  • · Replies 4 ·
Replies
4
Views
4K
MATLAB How to load data from the example supplied on MATLAB website?
  • · Replies 1 ·
Replies
1
Views
2K
MATLAB FEM, Matlab and the modes of an element
  • · Replies 32 ·
2
Replies
32
Views
4K
Graduate Runge Kutta finite difference of differential equations
  • · Replies 6 ·
Replies
6
Views
3K