roam
- 1,265
- 12
- Homework Statement
- What is the name of the following distribution, and why does increasing the exponent increase the magnitude variation?
- Relevant Equations
- Matlab code is shown below.
I have generated a distribution (normalized such that the sum is equal to 1) by using the code:
For an exponent ##z=1##, the sampling distribution is "flat", but it also has a shorter range. Enlarging ##z## gives a wider range of numbers. Why?
Here is a comparison of the results for ##z=1## and ##z=5##:
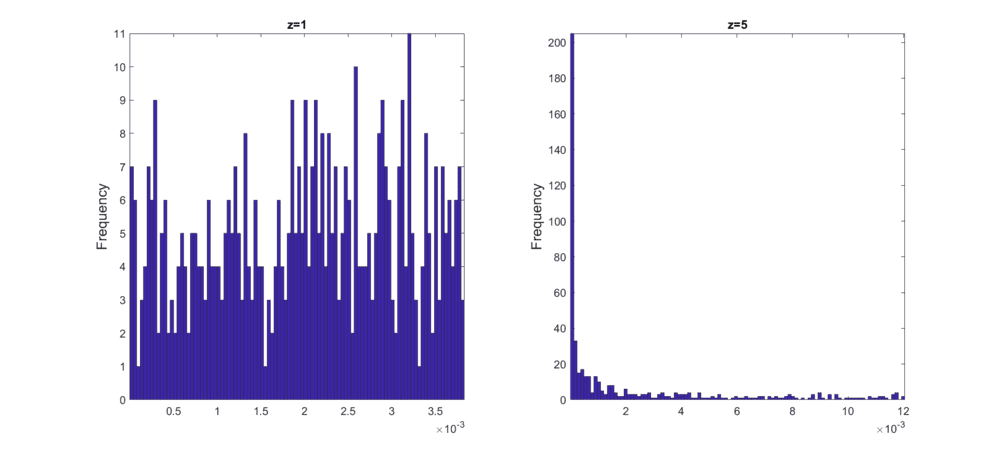
Also, is it possible to have both a wide range and a "flat" distribution at the same time (i.e. very large numbers being just as likely as the small numbers)?
Explanations would be greatly appreciated.
Matlab:
M=500; % Number of samples
z=1;
SUM = 1;
ns = rand(1,M).^z; % random numbers
TOT = sum(ns);
X = (ns/TOT)*SUM; % Re-scaling
hist(X(1,:),100)For an exponent ##z=1##, the sampling distribution is "flat", but it also has a shorter range. Enlarging ##z## gives a wider range of numbers. Why?

Here is a comparison of the results for ##z=1## and ##z=5##:
Also, is it possible to have both a wide range and a "flat" distribution at the same time (i.e. very large numbers being just as likely as the small numbers)?
Explanations would be greatly appreciated.