jarekduda
- 82
- 5
Due to required reversibility, classical function (f(a)=y^a \mod N) in Shor's algorithm needs a lot of auxiliary qubits. I was afraid that their later treatment might influence the computation - and just got confirmation from Peter Shor himself: that we need to "uncompute" these auxiliary qubits.
Let's look at quantum subroutine of Shor's algorithm:
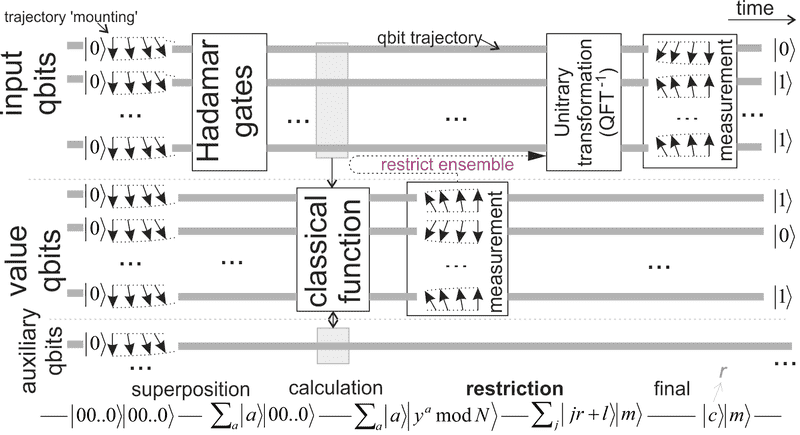
As measurement of value qubits has restricted the ensemble, measuring/collapse of auxiliary qubits should also affect the ensemble - this time in unwanted way.
I thought maybe we could "erase them" by measuring in orthogonal basis, but Peter Shor has replied:
"In order to make the factoring algorithm work properly, you need to reset all the auxiliary qubits, which started as |0⟩ at the beginning of the computation, to |0⟩ at the end of the computation. This is called "uncomputing" these qubits. (Actually, you can set them to anything you please as long as it is a constant independent of the workings of the algorithm.) Theorems about reversible classical computation ensure that it is possible to do this."
Asking for literature, he replied: "Measuring the qubits in the "orthogonal basis" isn't going to work. You need to "uncompute" them. This is discussed briefly on page 9 of my paper, and in much more detail in C. H. Bennett (1973), Logical reversibility of computation."
However, reversible computation of bits is just a permutation - I don't see how to "uncompute" most of them (auxiliary) to a fixed value such that the total process is still a permutation?
Can it be done? How? Have you seen addressed/solved this problem in a literature?
Let's look at quantum subroutine of Shor's algorithm:
- Hadamard gates create superposition of all (exponential number) values for input qubits.
- Then we perform a classical function on them, which is here: f(a)=y^a \mod N, where N is the number we would like to factorize, y is some chosen (usually random) number smaller than N
- Then we perform measurement of value of this function f(a)=m (random). This measurement restricts the original ensemble to only input values a, such that f(a)=m.
- Mathematics says that this restricted ensemble has to be periodic, this period can be concluded from value of (quantum) Fourier transform, and allows to conclude the factors.
As measurement of value qubits has restricted the ensemble, measuring/collapse of auxiliary qubits should also affect the ensemble - this time in unwanted way.
I thought maybe we could "erase them" by measuring in orthogonal basis, but Peter Shor has replied:
"In order to make the factoring algorithm work properly, you need to reset all the auxiliary qubits, which started as |0⟩ at the beginning of the computation, to |0⟩ at the end of the computation. This is called "uncomputing" these qubits. (Actually, you can set them to anything you please as long as it is a constant independent of the workings of the algorithm.) Theorems about reversible classical computation ensure that it is possible to do this."
Asking for literature, he replied: "Measuring the qubits in the "orthogonal basis" isn't going to work. You need to "uncompute" them. This is discussed briefly on page 9 of my paper, and in much more detail in C. H. Bennett (1973), Logical reversibility of computation."
However, reversible computation of bits is just a permutation - I don't see how to "uncompute" most of them (auxiliary) to a fixed value such that the total process is still a permutation?
Can it be done? How? Have you seen addressed/solved this problem in a literature?