Undergrad Significant correlation, not significant coefficient

[monsmatglad]

A couple of questions today. First. I am running a panel data regression test. First I check the correlations between the independent variables and the dependent variable. these are the results.

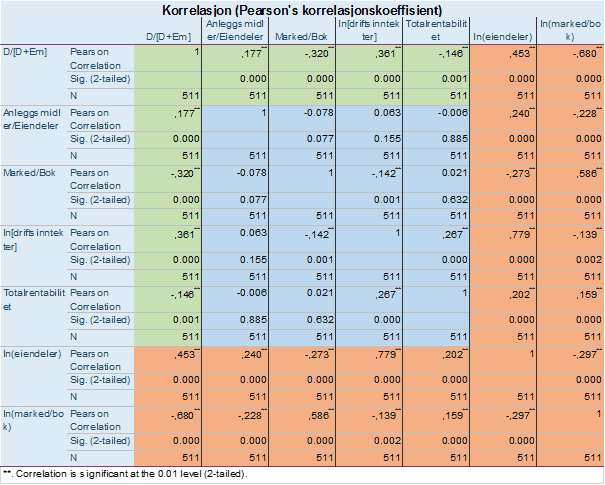
The D/(D+Em) is the dependent variable, and the independent are the 4 variables most adjacent. Disregard the two outer variables (the red area). The independent variable "Anleggsmidler/eiendeler" has a correlation coefficient (pearson's) to the dependent variable of ,177 and this is a very significant result as you can see. However, when I do the regression analysis (as shown below), the relation between "Anleggsmidler/eiendeler" and the dependent variable is not significant at all. How come the results are so different in terms of significance?

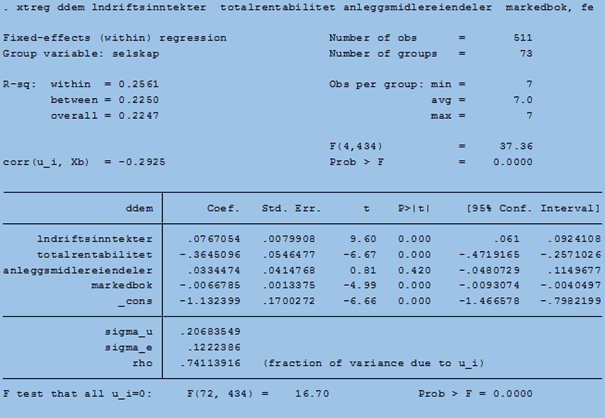
Second question is is there any command to include standardised coefficients to fixed effects regression results in stata? the beta command does not work when I use fixed effects regression (i am pretty green when it comes to Stata). Any advice on these two questions? Thanks in advance!

 

[Dale]

You have pretty substantial multicolinearity in this data. The estimates of individual coefficients will be unreliable in the regression.

 

[monsmatglad]

hey. I used a VIF-test and it produced the following numbers: I understand that it differs what is regarded as acceptable, but as far as I know, below 10 is usually no disaster (based on google searches, not on my acumen).

Variable VIF 1/VIF
lndriftsin~r 5.72 0.174921
anleggsmid~r 5.02 0.199399
totalrenta~t 1.34 0.743779
markedbok 1.18 0.845347
Mean VIF 3.31

 

[FactChecker]

By the time the (estimated) effects of the other variables are taken into account, there is not enough left for Anleggsmidler/eiendeler to be statistically significant. It should be removed from the model and the linear regression should be re-run without it.

 

[Dale]

I used a VIF-test

Instead, just try running a reduced model deleting totalrentabilitat