Discussion Overview
The discussion revolves around the question of how to prove the truth of the formula (∃x)(∃y)Rxy under a specific interpretation involving a finite domain. Participants explore the nature of satisfiability, the interpretation of logical formulas, and methods for demonstrating the truth of such formulas.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants clarify that a formula alone is neither true nor false without an interpretation, and that the meaningful question is whether the formula is true in a given interpretation.
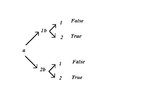
- One participant expresses confidence that there exists an 'x' and 'y' in {1,2} that satisfies the predicate 'R' and seeks a simple method to demonstrate this.
- Another participant notes that there is no general method for determining the truth of a formula in an interpretation, citing historical examples of complex formulas.
- One participant suggests that the problem can be approached mathematically by examining the relation defined by 'R' and its satisfaction by pairs from the domain.
- There is discussion about the need to understand the definition of truth in an interpretation, including concepts like valuation and substitution.
- Participants explore the possible pairs of values for 'x' and 'y' and how these relate to the truth values of the formula under the given interpretation.
Areas of Agreement / Disagreement
Participants generally agree that the formula can be shown to be true under the given interpretation, but there is no consensus on a universal method for proving the truth of formulas in interpretations. Some participants express uncertainty about specific steps and definitions involved.
Contextual Notes
There are limitations in the discussion regarding the clarity of definitions and the specific methods for demonstrating truth in interpretations. Some participants express confusion about the results of truth values for different instances of the variables.
Who May Find This Useful
This discussion may be useful for individuals interested in mathematical logic, particularly those exploring the concepts of satisfiability, interpretations, and the evaluation of logical formulas.