Smallest Set Containing All n-point Sets

[jgm340]

I've been thinking about this. Suppose you have an n-point set P in R^m which has the property that for any two points x, y in P, ||x - y|| < 2. If we fix n, what can we say about the smallest set S in R^m that contains P, allowing for both translations and orthogonal transformations of S?

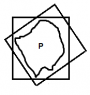
If we start in R², the answer is not what you'd expect! As illustrated in this picture, P must be able to fit inside of any 2 by 2 square after only translation:

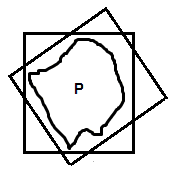
That is, if I were to have a square hoola-hoop, I could swing it around P. However, for n > 2, the intersection of all those squares would not necessarily fit inside a circle of diameter 2.

For n=2, the smallest set would be something like [0,1] U {2}.
For n=3, I think the smallest set would be {x = (x₁, x₂) : ||x - (0,1)|| < 2, x₁ < 0, x₂ < 0} U {x = (x₂,x₂) : x₁ = 0, -1 < x₂ < 1}

Any thoughts?

 

[radou]

I'm not sure what exactly you mean by "translations" and "orthogonal transformation".

If you have an n-point subset P of R^m, take max{||x - y||, x, y from P} = diam(P) = r = d(x0, y0) (for some x0, y0 in P), and then the closed ball B(x0, r) around x with radius r contains the set P.

 

[jgm340]

I'm not sure what exactly you mean by "translations" and "orthogonal transformation".

If you have an n-point subset P of R^m, take max{||x - y||, x, y from P} = diam(P) = r = d(x0, y0) (for some x0, y0 in P), and then the closed ball B(x0, r) around x with radius r contains the set P.

Yes, but that's not the smallest.
Take the intersection of the balls about x0 and y0. This would also necessarily contain P.

About the "translations and orthogonal transformations" business: I'm looking for a closed form for a set S which must "be able to contain" P. By "be able to contain", I mean that for any P, we ought to find some transformation T (involving only rotations, reflections, and translations) such that P is contained in T(S).