Discussion Overview
The discussion revolves around the conditions for two positive real numbers $x$ and $y$ that satisfy the equations $x^3=x+1$ and $y^6=3x+y$. Participants are tasked with demonstrating that $x>y$ under these conditions, exploring various approaches and reasoning.
Discussion Character
- Debate/contested
- Mathematical reasoning
Main Points Raised
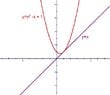
- Some participants propose to analyze the equations by comparing $y_1 = x^2 - x + 1$ and $y_2 = x$ for $x > 1$ to establish a relationship between $x$ and $y$.
- Others argue that while $y < x$ may hold true in some cases, specific values like $x = 1.7$ and $y = 1.8$ challenge this assumption, indicating that $y$ can be greater than $x$ despite the conditions.
- One participant suggests that the solution to the first equation must be found before substituting into the second equation to determine $y$, emphasizing the need for both $x$ and $y$ to satisfy their respective equations.
- There is a correction regarding an earlier mathematical claim about the equivalence of expressions, with participants acknowledging mistakes in their calculations.
- A later reply introduces an alternative solution method that does not rely on graphical approaches, although the details of this method are not elaborated upon.
Areas of Agreement / Disagreement
Participants express differing views on the relationship between $x$ and $y$, with some asserting $x > y$ while others present counterexamples that suggest this may not always hold. The discussion remains unresolved regarding the definitive relationship between the two variables.
Contextual Notes
Participants note that the values of $x$ and $y$ must meet the restrictions imposed by their respective equations, but the implications of specific values and their validity are debated without reaching a consensus.