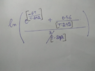
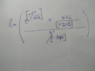
Solve ln(a/b+1) Using Identity ln(a+b)=ln b + ln(a/b+1)

[Gurasees]

How to solve "ln(a/b+1)" after applying the identity "ln(a+b)=ln b + ln(a/b+1)" ?
where "ln" is natural log, a and b have variable values in them.

 

[fresh_42]

What do you mean by "solve"?

 

[Gurasees]

What do you mean by "solve"?

The identity keeps repeating itself in the solution,
I want to take ln of

• {e^(-6.7/(T-292)) + 0.56/(T-292)} / {3/(T-292)}

 

[Gurasees]

 

[fresh_42]

So you have $\log \left( (T-292)\exp\left( \dfrac{-6.7}{T-292} \right) + 0.56 \right) - \log(3)\,.$
I think you can only solve this numerically, resp. expand the exponential function and the logarithm into power series, in which case you must consider the interval of convergence.

 

[Gurasees]

So you have $\log \left( (T-292)\exp\left( \dfrac{-6.7}{T-292} \right) + 0.56 \right) - \log(3)\,.$
I think you can only solve this numerically, resp. expand the exponential function and the logarithm into power series, in which case you must consider the interval of convergence.

I don't know how to do that. Can you send me some links which might be helpful for the solution?

 

[fresh_42]

I don't know how to do that. Can you send me some links which might be helpful for the solution?

Solution of what? You cannot simplify this expression further. To solve something, an equation would be helpful. You can find the power series on Wikipedia if you look for the exponential, resp. logarithmic function. But look out for the range of $T-292\,.$

 

[mfb]

I still don't see an equation you could solve. Can you "solve a+b"?
We have an expression that depends on T. Should that be equal to something specific? Do you want to find a T such that the expression will obtain a given value? That will need numerical approximations.

 

[Gurasees]

Solution of what? You cannot simplify this expression further. To solve something, an equation would be helpful. You can find the power series on Wikipedia if you look for the exponential, resp. logarithmic function. But look out for the range of $T-292\,.$

Solution of what? You cannot simplify this expression further. To solve something, an equation would be helpful. You can find the power series on Wikipedia if you look for the exponential, resp. logarithmic function. But look out for the range of $T-292\,.$

Thanks for your help.

 

[Gurasees]

Solution of what? You cannot simplify this expression further. To solve something, an equation would be helpful. You can find the power series on Wikipedia if you look for the exponential, resp. logarithmic function. But look out for the range of $T-292\,.$

I can't find the expansion of ln(x-a). Can you help?

 

[fresh_42]

I can't find the expansion of ln(x-a). Can you help?

https://en.wikipedia.org/wiki/Logarithm#Power_series

but be cautious with the range in which they can be applied. You have to have some knowledge about the quantity $T-292$.
In case you have an actual equation, I would let do wolframalpha the job: https://www.wolframalpha.com/