anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
Hi all,
I've tried to no avail to find the solution to this equation in exact form, and I'm giving it up entirely and I hope someone would come up with a brilliant idea on how to tackle it elegantly.
Thanks in advance.:)
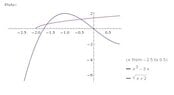
Problem: Solve $$x^3-3x=\sqrt{x+2}$$.
I've tried to no avail to find the solution to this equation in exact form, and I'm giving it up entirely and I hope someone would come up with a brilliant idea on how to tackle it elegantly.
Thanks in advance.:)
Problem: Solve $$x^3-3x=\sqrt{x+2}$$.