Solving a Problem: What Went Wrong & Velocity for Both Masses

  • Thread starter Thread starter Mohmmad Maaitah
  • Start date Start date
  • Tags Tags
    Velocity
AI Thread Summary
The discussion centers on a problem involving two connected masses and their velocities. The original poster is confused about their solution and whether the velocity is the same for both masses. Respondents clarify that while the masses are connected and share the same speed, they move in opposite directions. There is also a note that the provided solution incorrectly identifies the hanging mass. The key takeaway is that the velocities are indeed the same, despite the confusion over the mass designation.
Mohmmad Maaitah
Messages
90
Reaction score
20
Homework Statement
As in the first provided picture:
Relevant Equations
Newton second law
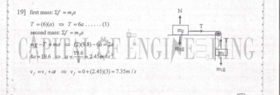
This is the problem:
1683368077531.png


And this the answer provided by the examiner:
1683367960587.png

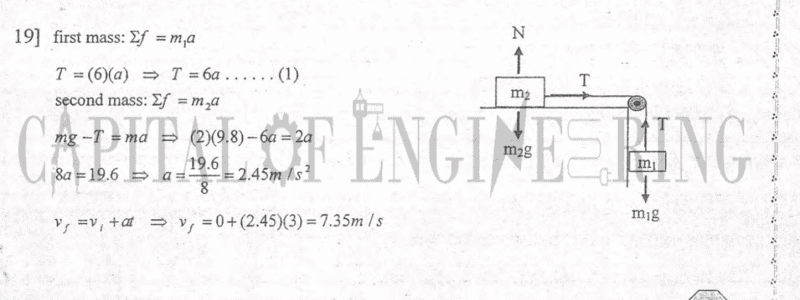
And this is my own answer:
IMG_20230506_130351_883.jpg


So what did I get wrong???
Also I want to know if the Velocity is the same for both masses.
 

Attachments

  • IMG_20230506_130351_883.jpg
    IMG_20230506_130351_883.jpg
    29.7 KB · Views: 98
  • 1683367838828.png
    1683367838828.png
    39.3 KB · Views: 101
  • 1683367894227.png
    1683367894227.png
    43.5 KB · Views: 97
Physics news on Phys.org
Mohmmad Maaitah said:
So what did I get wrong???
The diagram shows m_1 as the hanging mass, but the given solution switches that. Your work is fine.
Mohmmad Maaitah said:
Also I want to know if the Velocity is the same for both masses.
Sure---they are connected. (The speeds are the same, but they move in different directions, of course.)
 
Reply
  • Like
Likes Chestermiller and Mohmmad Maaitah
Doc Al said:
The diagram shows m_1 as the hanging mass, but the given solution switches that. Your work is fine.

Sure---they are connected. (The speeds are the same, but they move in different directions, of course.)
Oh lord, he switched the masses :doh:
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »

Similar threads

Query related to Two-Dimensional Motion
Replies
9
Views
1K
Ambiguous question on momentum and how it works...
Replies
13
Views
1K
projectile motion problem with no initial velocity given
Replies
3
Views
648
The gravitating of a small mass towards a big mass
Replies
3
Views
2K
Body attached to a block by a spring, shaped like an inclined plane
Replies
1
Views
882
Conservation of Energy with Gravitational Potential Energy
Replies
6
Views
2K
Coefficient of Restitution for a Hypothetical Collision where masses are not equal after the collision compared to before the collision
Replies
6
Views
1K
Equilibrium Position of a Hanging Candy Cane
Replies
17
Views
829
Test question: What is true for a mechanical impact?
Replies
7
Views
1K
Drag Forces and Terminal Velocity
Replies
8
Views
910

Hot Threads

Recent Insights

Back
Top