Cdn
- 1
- 0
I am a senior ecology undergraduate, this problem came up on the last assignment for my population ecology class. It's been a long time since I've done any probability, but I remember a bit and hope I'm on the right track.
There is a species of parasitic worm that inhabits the intestines of the moose, the eggs of this parasite exit the moose in the feces for all practical purposes every moose who has the parasite has eggs in the feces. The eggs however are not very numerous and only 20% of all slides prepared from an infected fecal sample will contain some. How many slides would a lab tech have to prepare and to examine per specimen, so that if a specimen is positive, there is a 99% probability that at least one slide will show eggs present in the slide?
I'm thinking that the binomial probability distribution would be appropriate as each trial (slide) has only two outcomes (positive, eggs present, 20%, p=0.2 or negative, eggs not present, 80%, q=0.8). p+q=1. The total number of slides = n. Since the problem is asking for probability of "at least one slide", it would be the additive probabilities of one slide + two slides +. . . + n slides (0.99) which is equal to the alternative 1-(the probability that 0 slides out of n contain eggs(0.01)). If my thinking is correct so far . . . I would be able to use this equation
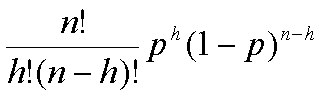 =0.01
=0.01
If I were to go with the 0 successful trials route the equation would equal 0.01, n=total number of trials (unknown in this situation), h=0, p=0.8.
From here I am stuck, I can't figure out how to solve for n.
I hope I'm on the right track.
Thanks
Homework Statement
There is a species of parasitic worm that inhabits the intestines of the moose, the eggs of this parasite exit the moose in the feces for all practical purposes every moose who has the parasite has eggs in the feces. The eggs however are not very numerous and only 20% of all slides prepared from an infected fecal sample will contain some. How many slides would a lab tech have to prepare and to examine per specimen, so that if a specimen is positive, there is a 99% probability that at least one slide will show eggs present in the slide?
Homework Equations
The Attempt at a Solution
I'm thinking that the binomial probability distribution would be appropriate as each trial (slide) has only two outcomes (positive, eggs present, 20%, p=0.2 or negative, eggs not present, 80%, q=0.8). p+q=1. The total number of slides = n. Since the problem is asking for probability of "at least one slide", it would be the additive probabilities of one slide + two slides +. . . + n slides (0.99) which is equal to the alternative 1-(the probability that 0 slides out of n contain eggs(0.01)). If my thinking is correct so far . . . I would be able to use this equation
If I were to go with the 0 successful trials route the equation would equal 0.01, n=total number of trials (unknown in this situation), h=0, p=0.8.
From here I am stuck, I can't figure out how to solve for n.
I hope I'm on the right track.
Thanks