Solving Gaussian Potential - Analyzing Energy Differences

[aaaa202]

Okay, I have solved the schrödinger equation numerically by making it dimensionless (though I am still confused about this proces). And then approximating it on a finite interval and solving the resulting eigenvalue equation. This allows me to solve for the wave function of different potentials.
I started with the harmonic oscillator but have no reached the Gaussian one:
V = -V₀exp(-x²)
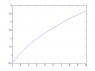
In one simulation I am asked to find the difference in energy between the ground state and the first excited state as a function of V₀. On the attached graph I have done this for V₀=1..2..3...10
Does it look right?
I am then asked the following: Solve the problem analytically by taylorexpanding the potential. So I taylor expand around x=0 to second order and find:
V(x) = -V₀ + V₀x²
Plugging this into my dimensionless Schrödinger equation I get:
½∂²ψ/∂x² + (-V₀ + V₀x²)ψ = Eψ
I thought aha. The x²-term can just be put in the harmonic oscillator form if we pick k=2V₀ and the -V₀ term will just shift the energy of the oscillator, not alter the difference between E1 and E0.
But in thinking it over again there are some problems. With my dimensionless equation I just had V(x)=½x² for the harmonic oscillator. Now I have 2V₀ in front of that. How will this constant effect my energies?
And is all this even the right procedure?

 

[mfb]

The difference in energy levels scales with the square root of the prefactor in a harmonic potential - in the dimensionless shape, this is hidden in the parameter transformations. In a region where this harmonic approximation is good (probably large V₀), I would expect that the difference grows with the square root of V₀, and your graph roughly looks like that. For small V₀, you probably get additional effects from higher orders of the potential.

 

[aaaa202]

okay but I am meant to show this analytically. How can I do that?

 

[mfb]

With the standard formulas for a harmonic oscillator. In your dimensionless version, you should have the conversion factors somewhere.
Or with the simple sqrt-dependence if you like.

 

[aaaa202]

well the conversion formula to dimensionless units is x' = x * √(mω/hbar)
So do I go back to formulate it all in terms of x? :S I am very confused sorry.

 

[mfb]

That is possible. Alternatively, you can extract the scale of V from that prefactor.

 

[aaaa202]

okay I did the problem and did indeed find that the difference went like √(2V0) - I am just curious - how is it you can see that the harmonic approximation is better for bigger v0?

 

[mfb]

Intuition. Deeper wells of the same size tend to have more bound states, so the lowest states are "deeper" in the well and smaller in terms of their size in x.