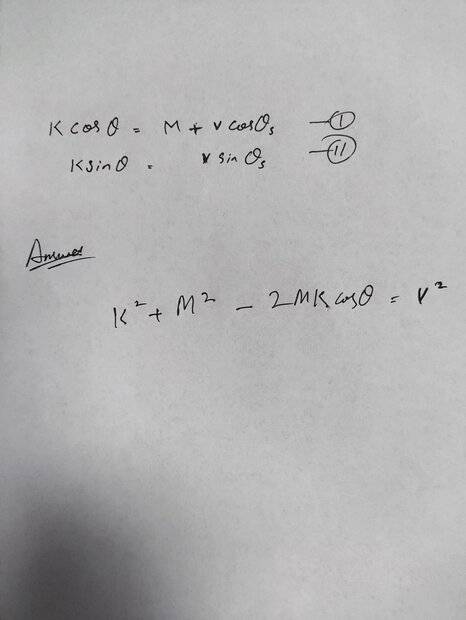SUMMARY
The discussion focuses on solving simultaneous equations involving sine and cosine functions, specifically using the identity \(\sin^2\theta + \cos^2\theta = 1\). Participants emphasize the importance of squaring both sides of the equations to simplify the problem. The solution involves expressing the variables \(V \sin\theta\) and \(V \cos\theta\) explicitly and applying the trigonometric identity effectively. The guidance provided leads to a clear resolution of the equations.
PREREQUISITES
- Understanding of trigonometric identities, specifically \(\sin^2\theta + \cos^2\theta = 1\)
- Ability to manipulate algebraic equations, including squaring both sides
- Familiarity with simultaneous equations and their solutions
- Basic knowledge of sine and cosine functions
NEXT STEPS
- Study the derivation and applications of the identity \(\sin^2\theta + \cos^2\theta = 1\)
- Learn techniques for solving simultaneous equations in trigonometry
- Explore advanced trigonometric identities and their proofs
- Practice problems involving the application of sine and cosine in various contexts
USEFUL FOR
Students studying trigonometry, educators teaching mathematical concepts, and anyone interested in solving trigonometric equations effectively.