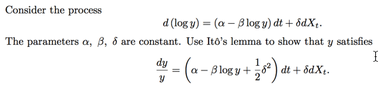Stochastic Differential Equation using Ito's Lemma
- Context: MHB
- Thread starter cdbsmith
- Start date
Click For Summary
This discussion focuses on the application of Ito's Lemma in the context of Stochastic Differential Equations (SDEs). The user cdbsmith seeks clarification on the steps involved in applying Ito's Lemma to a specific SDE, where the process is defined as $dY_t = \mu_t dt + \sigma_t\, dX_t$. The response provided by Euge explains the derivation of the formula using the function $g(u) = e^u$ and outlines the necessary conditions for the function $f(t, x)$ to satisfy the SDE. Key equations derived include $\frac{dy}{y} = (\alpha - \beta\log y + \frac{1}{2}\delta^2) dt + \delta\, dX_t$.
PREREQUISITES- Understanding of Stochastic Differential Equations (SDEs)
- Familiarity with Ito's Lemma and its applications
- Knowledge of Brownian motion and its properties
- Basic calculus, particularly differentiation and integration
- Study the derivation and applications of Ito's Lemma in various contexts
- Learn about the properties of Brownian motion and its role in SDEs
- Explore advanced topics in stochastic calculus, including semi-martingales
- Practice solving SDEs using different functions and conditions
Mathematicians, financial analysts, and researchers in quantitative finance or stochastic processes who are looking to deepen their understanding of Stochastic Differential Equations and Ito's Lemma.
Similar threads
- · Replies 3 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 7 ·
- · Replies 6 ·
- · Replies 1 ·
- · Replies 5 ·
- · Replies 2 ·