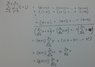AdityaDev
- 527
- 33
Homework Statement
##\sum\limits_{r=0}^n\frac{1}{^nC_r}=a##. Then find the value of $$\sum\sum\limits_{0\le i<j\le n}(\frac{i}{^nC_i}+\frac{j}{^nC_j})$$
Homework Equations
I have used two equations which I derived myself. This is the first one.
The second one is:
3. The Attempt at a Solution
Using first equation and second equation:
Now I have to subtract the cases where I=j to get the required sum. But Iis the above conclusion correct? Because I am not getting the required answer after subtracting.