- #1
havsula
- 22
- 2
Hello
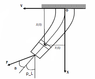
I have a system of differntial equations:
dx/ds = sin(p)
dy/ds=cos(p)
dp/ds = k
dk/ds = -1/EI(s)*(k*dEI/ds+f*sin(p))
x(0)=y(0)=p(0)=p(L)-pl = 0
These are nonlinear differential equations. I should use some sort of nonlinear finite difference. But I do struggle to setting up the finite difference system. I have found a lot of examples when we only have one differential equation for nonlinear finite difference.
But here I got 4 variables. Any suggestions?
I have a system of differntial equations:
dx/ds = sin(p)
dy/ds=cos(p)
dp/ds = k
dk/ds = -1/EI(s)*(k*dEI/ds+f*sin(p))
x(0)=y(0)=p(0)=p(L)-pl = 0
These are nonlinear differential equations. I should use some sort of nonlinear finite difference. But I do struggle to setting up the finite difference system. I have found a lot of examples when we only have one differential equation for nonlinear finite difference.
But here I got 4 variables. Any suggestions?