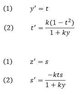System of two second order ODE's

[chenrim]

Hi ,
I have tried solving the following system of ODE's (eq1 attached) using Matlab.
first i reduced it into a system of four 1st order ODE's (eq2 attached).
thani tried to solve it using ode45() in the following manner:

function xprime = Mirage(t,x);
k=2;
xprime=[x(1); k*(1-x(1).^2)./(1+k*x(2)); x(3) ; -(k*x(1)*x(3))./(1+k*x(2))];
end

x0=[1 1 1 1];
tspan=[0,20];
[t,x]=ode45(@Mirage,tspan,x0)the program seem to be in infinite loop(stays Busy).
where did i wrong?
i will appreciate your help.

 

[da_nang]

You've got the order of the vector elements wrong. Matlab assumes the function \vec y&#039; = \vec f(t, \vec y). In other words, <br /> \left[ \begin{array}{ccc}<br /> y_1&#039; \\<br /> y_2&#039; \\<br /> y_3&#039; \end{array} \right] =<br /> \left[ \begin{array}{ccc}<br /> f_1(t, \vec y) \\<br /> f_2(t, \vec y) \\<br /> f_3(t, \vec y) \end{array} \right], \vec y =<br /> \left[ \begin{array}{ccc}<br /> y_1 \\<br /> y_2 \\<br /> y_3 \end{array} \right]<br /> and so on. The slowdown in your case is due to xprime's current setup wrecking havoc on ode45's adaptive step feature i.e. it's making the time step smaller and smaller.

 

[chenrim]

Hi da_nang thanks for your answer.
I think i didn't fully understand. In the Mirage function i set two inputs: the first one is the time interval for solving the problem.
the second will be a vector of initial conditions.
the line where " xprime=.." i must have mixed values of x(1) with x(2) and so on because the four equations are semi dependent.
how should the elements should be set? i'll be happy if you can post a fixed code.
thanks

 

[da_nang]

It's easier to show if you number your functions. \vec y =<br /> \left[ \begin{array}{ccc}<br /> y_1 \\<br /> y_2 \\<br /> y_3 \\<br /> y_4 \end{array} \right] =<br /> \left[ \begin{array}{ccc}<br /> y \\<br /> y&#039; \\<br /> z \\<br /> z&#039; \end{array} \right]<br />
This gives you the following system of ODEs. \vec y&#039; = \vec f(t, \vec y) \iff<br /> \left[ \begin{array}{ccc}<br /> y_1&#039; \\<br /> y_2&#039; \\<br /> y_3&#039; \\<br /> y_4&#039; \end{array} \right] =<br /> \left[ \begin{array}{ccc}<br /> y_2 \\<br /> \frac{k(1 - y_2^2)}{1 + k y_1} \\<br /> y_4 \\<br /> \frac{k y_2 y_4}{1 + k y_1}\end{array} \right]<br />

From this you can fix the code by swapping the indices 1 with 2 and 3 with 4.

 

[chenrim]

I tried your seggestion and it's still doesn't seem to work out for me..
is it working for you?

 

[da_nang]

Replace

xprime=[x(1); k*(1-x(1).^2)./(1+k*x(2)); x(3) ; -(k*x(1)*x(3))./(1+k*x(2))];

with

xprime=[x(2); k*(1-x(2).^2)./(1+k*x(1)); x(4) ; -(k*x(2)*x(4))./(1+k*x(1))];

.

The functions y and z are stored in

x(:,1)

and

x(:,3)

respectively after you've run the program. It should work.

 

[chenrim]

It's working , Thank you very much :)
appreciate your help !