.the blue from Tuesday does it have to be connected with the red of Thursday?

[evinda]

Hey! :)
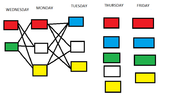
Adriana will be examinated in $5$ subjects, one at each day.She has $5$ dresses in different colors: red-blue-green-white-yellow. On Monday she does not want to wear the blue or green one.

On Tuesday, she does not wear the red or green one.

On Wednesday,she does not wear the blue, white or yellow one.

On Friday ,she does not wear the white one.

With how many different ways can Adriana be dressed,if she does not want to wear the same dress more than once?

I tried to solve it using this diagram:

View attachment 2582But..the blue from Tuesday does it have to be connected with the red of Thursday??

 

[Nono713]

Yes, this might not have been the best way to do it, because it makes it impossible to actually count the number of possibilities from the graph (or at least, it doesn't help you count them faster). Indeed, you need to connect (Tue, Blue) with (Thu Red) otherwise you would exclude the possibility (Wed, Green), (Mon, White), (Tue, Blue), (Thu, Red), but at the same time, if you do connect them then it looks like you are counting the (Wed, Green), (Mon, Red), (Tue, Blue), (Thu, Red) possibility which should not be counted because she can't wear the red dress twice.

Your graph should probably look more like a tree, where each choice of dress color for each day splits off into independent possibilities for the next day. Then you just need to count the number of paths in the tree (which, as you know, is the same as the number of leaves in the tree) and you are done. It might seem like the tree would be huge, but since she can't wear the same dress twice the possibilities are actually pretty limited.

Also I think the order matters here - there are combinations where she will have used all of the available dresses on the previous days and will have nothing to wear on that day (that she will want to wear). Since I assume turning up at the exam naked is not an option, you will need to recognize and handle these cases. I think a hybrid approach where you do part of the problem (say, three days out of five) with a graph and handle the remaining cases combinatorically might be a good approach.

 

[evinda]

Yes, this might not have been the best way to do it, because it makes it impossible to actually count the number of possibilities from the graph (or at least, it doesn't help you count them faster). Indeed, you need to connect (Tue, Blue) with (Thu Red) otherwise you would exclude the possibility (Wed, Green), (Mon, White), (Tue, Blue), (Thu, Red), but at the same time, if you do connect them then it looks like you are counting the (Wed, Green), (Mon, Red), (Tue, Blue), (Thu, Red) possibility which should not be counted because she can't wear the red dress twice.

Your graph should probably look more like a tree, where each choice of dress color for each day splits off into independent possibilities for the next day. Then you just need to count the number of paths in the tree (which, as you know, is the same as the number of leaves in the tree) and you are done. It might seem like the tree would be huge, but since she can't wear the same dress twice the possibilities are actually pretty limited.

Also I think the order matters here - there are combinations where she will have used all of the available dresses on the previous days and will have nothing to wear on that day (that she will want to wear). Since I assume turning up at the exam naked is not an option, you will need to recognize and handle these cases. I think a hybrid approach where you do part of the problem (say, three days out of five) with a graph and handle the remaining cases combinatorically might be a good approach.

I tried it know with a tree:

View attachment 2583

Is it right or have I done something wrong?
Each level of a tree represent a day..

So,are there $18$ different ways that Adriana can be dressed? (Thinking)

 

[I like Serena]

That looks right! :D

Here's an alternative way.
The generating polynomial is:
$$(r+w+y)(b+w+y)(r+g)(r+b+g+w+y)(r+b+g+y)$$
Since we're interested in different dresses for each day, we'll look at the coefficient of $bgrwy$.
See W|A, where you can see that the coefficient is $18$. (Cool)

 

[evinda]

That looks right! :D

Here's an alternative way.
The generating polynomial is:
$$(r+w+y)(b+w+y)(r+g)(r+b+g+w+y)(r+b+g+y)$$
Since we're interested in different dresses for each day, we'll look at the coefficient of $bgrwy$.
See W|A, where you can see that the coefficient is $18$. (Cool)

Great!Thank you very much! (Clapping)