SUMMARY
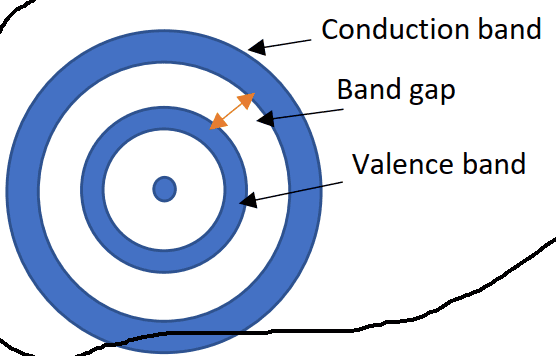
The discussion centers on the behavior of excited electrons in the conduction band, emphasizing that these electrons are not bound to a specific nucleus and can move freely over long distances. It is established that while higher-energy electrons are generally found farther from the nucleus, their exact position cannot be precisely determined due to quantum mechanics. The conversation highlights the distinction between classical and quantum mechanical interpretations of electron behavior, particularly in relation to band structure and conductivity.
PREREQUISITES
- Quantum mechanics fundamentals
- Understanding of conduction band theory
- Basic principles of electron behavior in solids
- Familiarity with band structure diagrams
NEXT STEPS
- Research quantum mechanics and electron localization
- Study the properties of conduction bands in semiconductors
- Explore band structure calculations using tools like VASP or Quantum ESPRESSO
- Learn about the implications of electron mobility on electrical conductivity
USEFUL FOR
Students and professionals in physics, materials science, and electrical engineering who are interested in the behavior of electrons in solid-state systems and the principles of conductivity.