- 37,402
- 14,234
On arXiv: The Significance Filter, the Winner's Curse and the Need to Shrink
It's well known that it is difficult to publish null results in various fields. The authors try to quantify that by analyzing over a million z-scores from Medline, a database for medical publications. A very striking result is figure 1, red lines and numbers were added by me:
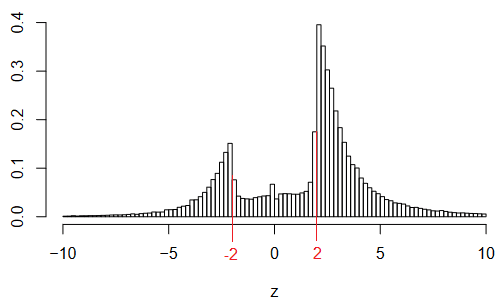
The infamous two-sided p<0.05 is at z=1.96. We see a really sharp edge, if the bin edge were at 1.96 instead of 2 it would look even more pronounced.
Should we expect a normal distribution? No. That would be the shape if nothing depends on anything ever. Things do depend on each other, so the tails are larger. It's perfectly fine to start a study where earlier results suggest you'll end up with a z-score around 2 for example. But we certainly should expect a smooth distribution - in a well-designed experiment the difference between z=1.9 and z=2.1 is purely random chance.
If 10 groups take measurements of something that's uncorrelated, one of them finds z>2 by chance and only that one gets published we get a strong bias in the results. p-hacking leads to a similar result as selective publishing. Things look important where the combined measurements would clearly show that there is nothing relevant. Even worse, meta-analyses will only take the published results, calculating an average that's completely disconnected from reality.
The authors quantify some problems that arise from selective publishing.
It's well known that it is difficult to publish null results in various fields. The authors try to quantify that by analyzing over a million z-scores from Medline, a database for medical publications. A very striking result is figure 1, red lines and numbers were added by me:
The infamous two-sided p<0.05 is at z=1.96. We see a really sharp edge, if the bin edge were at 1.96 instead of 2 it would look even more pronounced.
Should we expect a normal distribution? No. That would be the shape if nothing depends on anything ever. Things do depend on each other, so the tails are larger. It's perfectly fine to start a study where earlier results suggest you'll end up with a z-score around 2 for example. But we certainly should expect a smooth distribution - in a well-designed experiment the difference between z=1.9 and z=2.1 is purely random chance.
If 10 groups take measurements of something that's uncorrelated, one of them finds z>2 by chance and only that one gets published we get a strong bias in the results. p-hacking leads to a similar result as selective publishing. Things look important where the combined measurements would clearly show that there is nothing relevant. Even worse, meta-analyses will only take the published results, calculating an average that's completely disconnected from reality.
The authors quantify some problems that arise from selective publishing.