The spin of the neutron is a quantized property

[borib]

TL;DR

I ask about a physics experiment about the neutrons and the spin property.

In the brilliant.org website talking about quantum properties it is said that neutrons coming from a nuclear oven and passing through two permanent magnets of opposite polarity hit a surface only at the top and the bottom of it (there is no continuity) because the spin property is quantized and the neutrons trajectory are deviated either at the top or the bottom extremities because the spin axis is either at 90 degree or -90 degree.

My question is: is it possible that the spin axis can exist also at 35, -35, 20, -45... degrees but as soon as the neutron pass through the magnets the spin axis is immediately rotated at 90 or -90 degrees?

That would mean that the spin is not quantized and the neutrons exiting the oven can have a spin axis of random degree, but it will look like the neutrons hitting the surface are only 90 and -90 degrees.

 

[Nugatory]

My question is: is it possible that the spin axis can exist also at 35, -35, 20, -45... degrees but as soon as the neutron pass through the magnets the spin axis is immediately rotated at 90 or -90 degrees?

It is not possible, but this particular experiment is not sufficent to show that.

The quantum description of this process says that the magnitude of the neutron's spin is fixed but the direction of the spin is not defined. Note that that's not "unknown" or "some random value and we don't know what it is but it rotates to +/- 90 degrees when it interacts with the magnetic field", it is really literally "not defined" - it is meaningless to talk about its value until the interaction with the magnetic field happens.

It turns out that there are subtle statistical differences between the "undefined" behavior predicted by quantum mechanics and the "immediately rotates to 90 or -90 degrees" behavior that you're considering. These differences can be tested exerimentally, the experiments have been done, and they've confirmed the quantum mechanical prediction. For more information you will want to google for "Bell's theorem"; https://static.scientificamerican.com/sciam/assets/media/pdf/197911_0158.pdf and https://www.drchinese.com/Bells_Theorem.htm (by our own @DrChinese) are good starting points.

 

[PeroK]

Summary:: I ask about a physics experiment about the neutrons and the spin property.

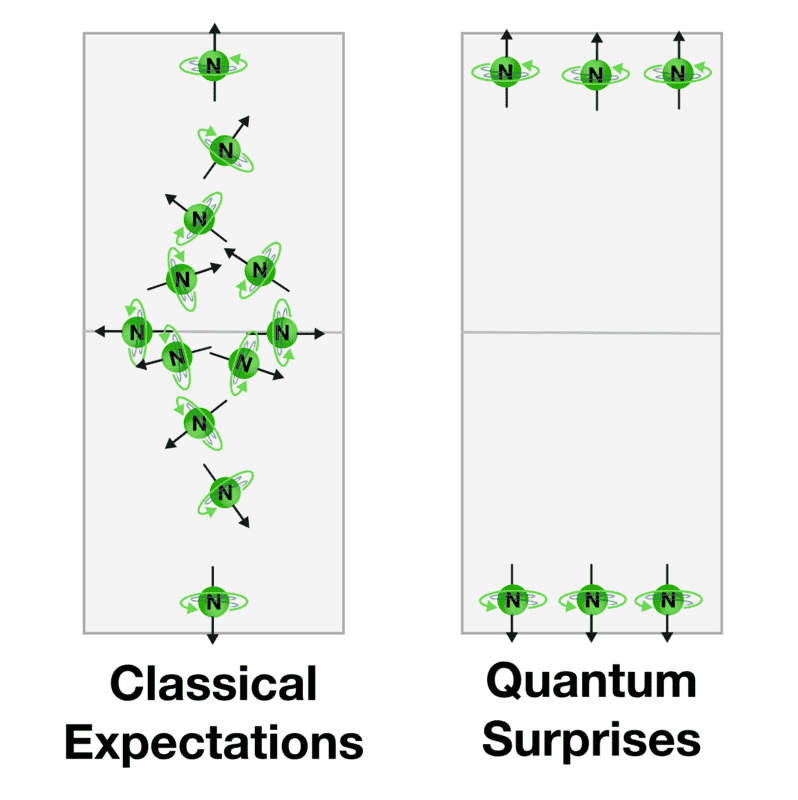
My question is: is it possible that the spin axis can exist also at 35, -35, 20, -45... degrees but as soon as the neutron pass through the magnets the spin axis is immediately rotated at 90 or -90 degrees?

That would mean that the spin is not quantized and the neutrons exiting the oven can have a spin axis of random degree, but it will look like the neutrons hitting the surface are only 90 and -90 degrees.

In orthodox QM, a particle such as a neutron does not have well-defined dynamic properties until a measurement is made. Asking, for example, how much spin a particle has about a given axis doesn't make sense except as the result of a measurement.

Instead, a particle's spin is described by a spin state, which specifies the probability of getting either of the two quantised values.

This is fundamental to the theory of QM.

Trying to impose well-defined spin states independent of measurement comes under the category of local hidden variable theories. An theorem devised by John Bell was designed to test the difference between local variable theories and QM, exploiting the different way probabilities arise in the two cases. Subsequent experiments showed that QM was correct and local hidden variable theories are not compatible with experiment results.

There are lots of threads on here and around the Internet on Bell's Theorem.

 

[arkantos]

Good morning guys, pardon me for the intrusion. I take the opportunity to ask a question in this conversation rather than publish a new post.
If the spin of particles is an intrinsic propriety, and any kind of particle has its own value spin, how the value of the spin of any particle has been calculated? How the spin-statistic theorem was formulated?
Experimentally, how bosons show to have interger spin values? How fermions half-integer?

 

[PeterDonis]

how the value of the spin of any particle has been calculated?

It's not calculated, it's measured. Neutrons, for example, are assigned the value of spin 1/2 because that's the magnitude of the spin we get whenever we measure it.

How the spin-statistic theorem was formulated?

This question should be asked in a separate thread; it's too far off topic for this one.

Experimentally, how bosons show to have interger spin values? How fermions half-integer?

By measuring them. See above.

 

[SergioPL]

It seems experimental physics has shown that either the “elements of reality” do not exist, or they can be used to describe a very limited set of features, not the whole reality.

However, I think another interpretation of what is a "hidden variable" is possible: the wave function is the [infinite] set of hidden variables for a particle: if we take the Dirac spinor, it defines the density of probability, density of momentum and spin orientation at each point, however, the wave function cannot be measured as a whole because: (1) any measurement of position or momentum is only able to provide a single quantity (for the position, momentum, spin…) while the wave function is not limited to a single point / momentum / spin orientation. (2) The particle measurement alters the original quantum state (3) the single measurement has a limited resolution so the "value" provided has an error range.

This way, we can think of the wave function as an “underlying reality” for the particle, something that we will never be able to fully know for a real particle but whose evolution can be described by the Hamiltonian. However, the wave functions do not seem to be capable to predict quantum entanglement effects, it seems something else should be added to indicate that two different wave functions (i.e. two particles) are entangled one another.

Regarding the spin, I wonder if a Pauli / Dirac wave function with disarranged spin would align with an external uniform magnetic field as the effect of the magnetic field Hamiltonian, in that case, we could have a well-defined magnitude.

 

[PeterDonis]

Moderator's note: Thread moved to quantum foundations and interpretations forum.

 

[PeterDonis]

I think another interpretation of what is a "hidden variable" is possible

Before trying to roll your own interpretation, I strongly suggest that you spend some time reading the literature on already existing interpretations of QM. You are certainly not the first person to struggle with trying to figure out what our quantum experiments are telling us about what is "really going on".

 

[Nugatory]

However, the wave functions do not seem to be capable to predict quantum entanglement effects, it seems something else should be added to indicate that two different wave functions (i.e. two particles) are entangled one another.

A quantum mechanical system containing two particles has a single wave function, not two wave functions that are "added together"; this is an fundamental aspect of the quantum mechanical treatment of multi-particle systems. Entanglement effects are predicted by this wave function just fine. For more information you might try googling for "entanglement non-factorizable".

However, I think another interpretation of what is a "hidden variable" is possible:...

The forum rules require a link to a paper in an appropriate peer-reviewed journal or other acceptable source before we can discuss such alternatives. If you can provide such a link we can continue the discussion, but otherwise the discussion will be closed.