TikZ: Clebsch-Gordon Table Generator

[topsquark]

I did this for some work I'm doing and I thought I'd offer the program in case anyone might want it. (And one little question.)

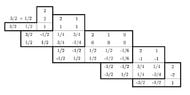
It's a Clebsch-Gordon table generator for addition of quantum angular momentums. The TikZ coding is fairly basic, but it's probably my best TikZ work so far, not because it was so difficult to program, but because of the limitations of the TikZ Mathematics engine. (Apparently, you can't calculate (-1)^n, even if you declare n to be an integer variable, because TikZ uses a logarithm to calculate it.) I had to be innovative in a couple of cases!

My question: One of the headaches I had was converting a decimal to a fraction. Now, it's a simple process, but I found out that TikZ does not automatically use a fixed point system, and TikZ does not allow for a while loop.

That's my question. In order to convert a decimal to a fraction my plan was to start with a possible denominator of 2, multiply the number by 2, and see if I got an integer. If so, I'm done. If not, add 1 to the denominator and loop around to do it again.

I did this all the way back in 11th grade when Apple IIs were still a thing. It's not hard. BUT in BASIC I could just simply use GOTO statements to do the loop, and when I took FORTRAN we used a WHILE loop. In TikZ I had to use a FOR loop and you have to set an upper limit on size of the denominator you want to use.
Say we have num = 0.25.

10 d = 2
20 If int(num*d) <> num*dd then d = d + 1; GOTO 20
30 end

or

d = 2
do while int(num*d) <> num*d
d = d + 1
end do

Both give d = 4.

My only solution was to do this:

stop = 0
for x = 2 to 20
if stop = 0 then
if int(num*x) = num*d then d = x; stop = 1
end if
end for

Again, I get d = 4, but if the denominator needs to be bigger than 20 it won't work.

Does anyone have a better solution?

One flaw in the program is that it doesn't print the table in landscape on the output so the table size is limited. I didn't need any large tables so I didn't bother to fix that. And I haven't a clue how to spread this to more than a single page.

Spin inputs are at the top of the "Defined Variables" box.

The TikZ code is in the next post.

-Dan

 

[topsquark]

(Reply to the post to see the code spacing properly.)
Moderator's note: I have added code tags. Please use them (it also conserves the spacing).

\usepackage{tikz,fp}
\usetikzlibrary{math,fixedpointarithmetic}
\begin{tikzpicture}[fixed point arithmetic]
% Variables
%    j1, m1, j2, m2: Input spin vectors
%    jtot, mtot: Total spin vector
%    jttot, mttot, mt1, mt2: Temporary spin vector values for the coeff function
%    blocks: Number of coefficient boxes
%    dw, dh: Number of cells per per box
%    aoldx, aoldy: Coordinates of the top right of the last coeefficient grid
%    anewx, anewy: Coordinates of the top right of the new coefficient grid
%    num: Number to be converted to fraction
%    r: Returned fraction
%    w, h: Width and height of one cell
%    max: Largest value of ki in the coefficient calculation
%===============================================================
% Program Block
%===============================================================
     \tikzmath {
%===============================================================
% Defined Variables
%===============================================================
          \j1=3/2; \j2=1/2;
          \w=1.2; \h=0.6;
          \m1=\j1; \m2=\j2;
          \jtot=\j1+\j2; \mtot=\jtot;
          \blocks=2*(\j1+\j2)+1;
%===============================================================
% Convert A Decimal To A Fraction
%===============================================================
          function f(\num) {
               integer \n, \d;
               \stop=0;
               for \k in {1,...,20} {
                    \a=round(10*round(1000*(\k*\num+0.001))/1000)/10;
                    if \stop==0 then {
                         if int(abs(\a))==abs(\a) then {
                              if \k==1 then {\n=\a; let \r="\n"; \stop=1; }
                                   else {\n=\a; \d=\k; let \r="\n/\d"; \stop=1; };
                         };
                    };
               };
               return \r;
          };
%===============================================================
% Calculate Coefficients
%===============================================================
          function coeff(\jttot,\mttot,\mt1,\mt2) {
               \b1=0; \b2=0; \b3=0; \b4=0; \b5=0;
               \e1=0; \e2=0; \e3=0; \e4=0; \e5=0;
               \stop1=0; \stop2=0; \stop3=0; \stop4=0; \stop5=0;
               for \g in {0,...,10} {
%===============================================================
%      Lower Summation Limit
%===============================================================
                    if \stop1==0 then {
                         if \j1+\j2-\jttot-\g>=0 then {\e1=\g; \stop1=1; };
                    };
                    if \stop2==0 then {
                         if \j1-\mt1-\g>=0 then {\e2=\g; \stop2=1; };
                    };
                    if \stop3==0 then {
                         if \j2+\mt2-\g>=0 then {\e3=\g; \stop3=1; };
                    };
                    if \stop4==0 then {
                         if \jttot-\j2+\mt1+\g>=0 then {\e4=\g; \stop4=1; };
                    };
                    if \stop5==0 then {
                         if \jttot-\j1-\mt2+\g>=0 then {\e5=\g; \stop5=1; };
                    };
                    if \e1>\e2 then {\v=\e1; } else {\v=\e2; };
                    if \v<\e3 then {\v=\e3; };
                    if \v<\e4 then {\v=\e4; };
                    if \v<\e5 then {\v=\e5; };
%===============================================================
%      Upper Summation Limit
%===============================================================
                    if \j1+\j2-\jttot-\g>=0 then {\b1=\g; };
                    if \j1-\mt1-\g>=0 then {\b2=\g; };
                    if \j2+\mt2-\g>=0 then {\b3=\g; };
                    if \jttot-\j2+\mt1+\g>=0 then {\b4=\g; };
                    if \jttot-\j1-\mt2+\g>=0 then {\b5=\g; };
                    if \b1<\b2 then {\p=\b1; } else {\p=\b2; };
                    if \p>=\b3 then {\p=\b3; };
                    if \p>=\b4 then {\p=\b4; };
                    if \p>=\b5 then {\p=\b5; };
               };
               \s=0;
               for \b in {\v,...,\p} {
                    \z=-1;
                    for \c1 in {0,...,\b} {
                         \z=\z*(-1);
                    };
                    \s=\s+\z/((\b)!*(\j1+\j2-\jttot-\b)!*(\j1-\mt1-\b)!*(\j2+\mt2-\b)!*(\jttot-\j2+\mt1+\b)!*(\jttot-\j1-\mt2+\b)!);
                    \z=\z*(-1);
               };
               \c=sqrt((2*\jttot+1)*(\jttot+\j1-\j2)!*(\jttot-\j1+\j2)!*(\j1+\j2-\jttot)!/(\j1+\j2+\jttot+1)!);
               \c=\c*sqrt((\jttot+\mttot)!*(\jttot-\mttot)!*(\j1-\mt1)!*(\j1+\mt1)!*(\j2-\mt2)!*(\j2+\mt2)!);
               \c=\c*\s;
               return \c;
          };
%===============================================================
% Spin Title
%===============================================================
          \aoldx=0; \aoldy=0;
          \p=f(\j1); \q=f(\j2); let \r = \p \, + \q; {\node at ({\aoldx-\w},{\aoldy+\h/2}) {\r}; };
%===============================================================
% Box Loop
%===============================================================
          for \i in {1,...,\blocks} {
%===============================================================
%      J Block Settings
%===============================================================
               \wjtot=\jtot; \c=0; \stop=0;
               for \x in {0,...,2*\jtot} {
                    if \stop==0 then {
                         if \wjtot>=\mtot then {\c=\c+1; };
                         if \wjtot<=-\mtot then {\stop=1; };
                         \wjtot=\wjtot-1;
                    };
               };
               \dw=\c;
%===============================================================
%      m1, m2 Block Settings
%===============================================================
               \hm1=\m1; \c=0;
               for \x in {0,...,2*\m1} {
                    if -\m2>\mtot-(\m1-\x) then {\hm1=\hm1-1; };
                    if \m2<\mtot-(\m1-\x) then {\c=\c+1; };
               };
               \dh=(2*\m1+1)-(\m1-\hm1)-\c;
               if \i==1 then {\dw=1; \dh=1; \hm1=\m1; };
               if \i==\blocks then {\dw=1; \dh=1; \hm1=-\m1; };
%===============================================================
%      Boxes and Spin States
%===============================================================
               \anewx=\aoldx+\dw*\w; \anewy=\aoldy-\dh*\h;
               {\draw (\aoldx,\aoldy) rectangle (\anewx,\anewy); };
               {\draw[line width=2pt] (\aoldx,\aoldy) -- ++ ({-2*\w},0) -- ++(0,-\dh*\h) -- ++ ({2*\w+\dw*\w},0) -- ++(0,{2*\h+\dh*\h}) -- ++(-\dw*\w,0) -- cycle; };
               for \t in {0,...,\dw-1} {
                    for \k in {0,...,\dh-1} {
                         \p=f(\jtot-\t); \q=f(\mtot); {\node at ({\aoldx+\w/2+\t*\w},{\aoldy+3*\h/2}) {\p}; \node at ({\aoldx+\w/2+\t*\w},{\aoldy+\h/2}) {\q}; };
                         \p=f(\hm1-\k); \q=f(\mtot-(\hm1-\k)); {\node at ({\aoldx-3*\w/2},{\aoldy-\h/2-\k*\h}) {\p}; \node at ({\aoldx-\w/2},{\aoldy-\h/2-\k*\h}) {\q}; };
                         \p=coeff(\jtot-\t,\mtot,\hm1-\k,\mtot-(\hm1-\k));
                         \x=1; if \p<0 then {\x=-1; };
                         \q=f(\x*(round(10000*(\p*\p))/10000)); { \node at ({\aoldx+\w/2+\t*\w},{\aoldy-\h/2-\k*\h}) {\q}; };
                    };
               };
               \mtot=\mtot-1;
               \aoldx=\anewx; \aoldy=\anewy;           
          };
    };
%===============================================================
\end{tikzpicture}

-Dan

 

[PhDeezNutz]

I can’t offer any substantive feedback but I very much appreciate your efforts. Angular momentum addition in QM (especially various kinds of Spin and Orbit) has always been a stumbling block for me. Perhaps with your program I’ll be able to see the underlying structure of CG tables.

Again, I appreciate it very much.

 

[topsquark]

I can’t offer any substantive feedback but I very much appreciate your efforts. Angular momentum addition in QM (especially various kinds of Spin and Orbit) has always been a stumbling block for me. Perhaps with your program I’ll be able to see the underlying structure of CG tables.

Again, I appreciate it very much.

You are welcome.

Actually, I don't think this will help you that much, except to generate some solutions for you to check. I used a general formula to get the coefficients rather than a method and the formula really doesn't tell you all that much.

I'd recommend this video. It should give you a reasonable review of what you need to fill in the tables. For the general theory I'd recommend something on the order of Sakuri's QM textbook.

-Dan