sha1000
- 125
- 6
- TL;DR
- Time dilation as a function of distance from the center of galaxy.
Hello everyone
- The gravitational force near the edge of the galaxy at point A (see attached image) can be calculated by assuming that all the galactic mass is located in the center of the galaxy.
- In order to calculate the gravitational force in the middle of the galaxy (point B) we take into account only the inner volume mass and we can neglect all the mass in outer volume.
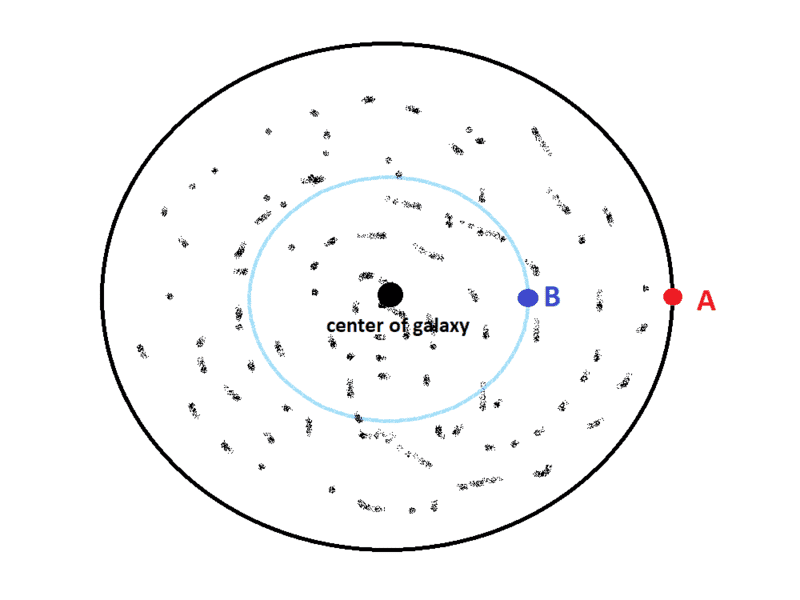
Can we apply the same logic for the gravitational time dilation?
What is the mass which I must use for the calculation of the time dilation at the point B? Do I need to take into account only the inner mass?
Thank you in advance.
- The gravitational force near the edge of the galaxy at point A (see attached image) can be calculated by assuming that all the galactic mass is located in the center of the galaxy.
- In order to calculate the gravitational force in the middle of the galaxy (point B) we take into account only the inner volume mass and we can neglect all the mass in outer volume.
Can we apply the same logic for the gravitational time dilation?
What is the mass which I must use for the calculation of the time dilation at the point B? Do I need to take into account only the inner mass?
Thank you in advance.