John Creighto
- 487
- 2
Trade: Production Possibility Boundaries
Many years ago in an economics class I remember learning about production possibility boundaries as a model of international trade.
http://tutor2u.net/economics/revision-notes/as-markets-production-possibility-frontier.html
I was thinking a bit about how these models may very with time.
A simple production possibility boundary would be an ellipse.
Consider a two nation model:
1) {x^2 \over C_{x,1}^2}+{y^2 \over C_{y,1}^2}=1
2) {x^2 \over C_{x,2}^2}+{y^2 \over C_{y,2}^2}=1
Each country would try to find the optimal consumption based on some objective function. A simple objective function is a hyperbola function which is equivalent to the function:
3) y=J/x <=> xy=J
Where J is the objective function (AKA utility function)
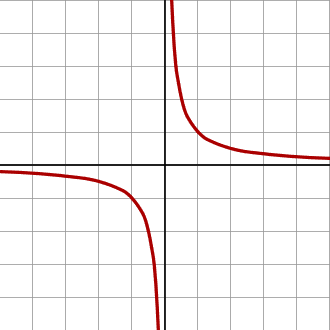
If there is no trade then each country tries to maximize J.
Subsituting 3) into equations 1) and 2) gives:
4) {x^2 \over C_{x,1}^2}+{{J_1/x}^2 \over C_{y,1}^2}=1
5) {x^2 \over C_{x,2}^2}+{{J_2/x}^2 \over C_{y,2}^2}=1
Multiplying both sides by x^2 and rearranging:
6) {x^4 \over C_{x,1}^2}-x^2+{J^2 \over C_{y,1}^2}=0
7) {x^4 \over C_{x,2}^2}-x^2+{J^2 \over C_{y,2}^2}=0
These equations have roots:
8) x_1^2={1 \pm \sqrt{1-{4 J_1^2 \over C_{x,1}^2 C_{y,1}^2}} \over {2 \over C_{x,1}^2}}9) x_2^2={1 \pm \sqrt{1-{4 J_2^2 \over C_{x,2}^2 C_{y,2}^2}} \over {2 \over C_{x,2}^2}}
Since x must be in the top right quadrant x is taken as positive and the positive square root is taken.
J can be found by setting setting the describable equal to zero in equations 8) and 9) to give:
10){1-{4 J_1^2 \over C_{x,1}^2 C_{y,1}^2}=011) {1-{4 J_2^2 \over C_{x,2}^2 C_{y,2}^2}=0
Which gives:
12)J_1={C_{x,1} C_{y,1} \over 2}13) J_2={C_{x,2} C_{y,2} \over 2}
Now with regards to trade each nation starts at their equilibrium given by equations: 1), 2), 8), 9), 12), 13)
That is:
x_1={C_{x,1} \over \sqrt{2}}
y_1={C_{y,1} \over \sqrt{2}}
x_1={C_{x,2} \over \sqrt{2}}
y_1={C_{y,2} \over \sqrt{2}}
And moves along their production possibility in exchange for receiving goods from the other nation. (More to come ...)
Many years ago in an economics class I remember learning about production possibility boundaries as a model of international trade.
http://tutor2u.net/economics/revision-notes/as-markets-production-possibility-frontier.html
I was thinking a bit about how these models may very with time.
A simple production possibility boundary would be an ellipse.
Consider a two nation model:
1) {x^2 \over C_{x,1}^2}+{y^2 \over C_{y,1}^2}=1
2) {x^2 \over C_{x,2}^2}+{y^2 \over C_{y,2}^2}=1
Each country would try to find the optimal consumption based on some objective function. A simple objective function is a hyperbola function which is equivalent to the function:
3) y=J/x <=> xy=J
Where J is the objective function (AKA utility function)
If there is no trade then each country tries to maximize J.
Subsituting 3) into equations 1) and 2) gives:
4) {x^2 \over C_{x,1}^2}+{{J_1/x}^2 \over C_{y,1}^2}=1
5) {x^2 \over C_{x,2}^2}+{{J_2/x}^2 \over C_{y,2}^2}=1
Multiplying both sides by x^2 and rearranging:
6) {x^4 \over C_{x,1}^2}-x^2+{J^2 \over C_{y,1}^2}=0
7) {x^4 \over C_{x,2}^2}-x^2+{J^2 \over C_{y,2}^2}=0
These equations have roots:
8) x_1^2={1 \pm \sqrt{1-{4 J_1^2 \over C_{x,1}^2 C_{y,1}^2}} \over {2 \over C_{x,1}^2}}9) x_2^2={1 \pm \sqrt{1-{4 J_2^2 \over C_{x,2}^2 C_{y,2}^2}} \over {2 \over C_{x,2}^2}}
Since x must be in the top right quadrant x is taken as positive and the positive square root is taken.
J can be found by setting setting the describable equal to zero in equations 8) and 9) to give:
10){1-{4 J_1^2 \over C_{x,1}^2 C_{y,1}^2}=011) {1-{4 J_2^2 \over C_{x,2}^2 C_{y,2}^2}=0
Which gives:
12)J_1={C_{x,1} C_{y,1} \over 2}13) J_2={C_{x,2} C_{y,2} \over 2}
Now with regards to trade each nation starts at their equilibrium given by equations: 1), 2), 8), 9), 12), 13)
That is:
x_1={C_{x,1} \over \sqrt{2}}
y_1={C_{y,1} \over \sqrt{2}}
x_1={C_{x,2} \over \sqrt{2}}
y_1={C_{y,2} \over \sqrt{2}}
And moves along their production possibility in exchange for receiving goods from the other nation. (More to come ...)
Last edited: