Triangle Area Based on Segment Division

[nolachrymose]

Hi all,

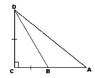
I'm working on this problem in my Geometry class, and am having a bit of trouble coming to a conclusion. The problem as given is (I've attached the figure to this thread):

In this figure, <ACD is a right angle. A, B, and C are collinear, <A = 30, and <DBC = 45. If AB = 3 - sqrt(3), find the area of triangle BCD.

From this information, I have deduced that triangle DCB is right isosceles, with DC = CB. Also, since <DBC and <DBA are supplementary (by LPP), <DBA = 135, and thus, by Triangle Sum Theorem, <BDA = 15. Then, by AAP, this means that <CDA = 60, and thus triangle ADC is a 30-60-90 right triangle.

I've gotten to this point, and I know the ratios of this special triangle, but I'm having trouble forming the right equations. I was wondering if anyone could give me a lead onto which I could follow.

Thanks a lot! :)

 

[nolachrymose]

Nevermind, I figured it out! :)
For anyone who wants to know how I solved it, this is how I did it:

I assigned "x" as the length DC and CB. Since triangle ADC is a 30-60-90 right triangle, the hypotenuse (DA) must be 2x. Then, using Pythagorean theorem, I derived the following equation:

(2x)^2 - x^2 = (x + 3 - \sqrt{3})^2
4x^2 - x^2 = (x + 3 - \sqrt{3})^2
3x^2 = (x + 3 - \sqrt{3})^2
x\sqrt{3} = x + 3 - \sqrt{3}
x\sqrt{3} - x = 3 - \sqrt{3}
x(\sqrt{3} - 1) = 3 - \sqrt{3}
x = \frac{3 - \sqrt{3}}{\sqrt{3} - 1}
x = \sqrt{3}

From there, I used x^2/2 = area of triangle BCD, so I got 3/2.

By the way, how do I do multi-line LaTeX equations? I tried using the "\\" symbol, both at the end of the previous line and at the start of the next line, and neither worked? (I ended up using multiple [ itex ] tags to get the effect I wanted.)

 

[M98Ranger]

Hi there,

It seems like you are on the right track with your deductions. To find the area of triangle BCD, we can use the formula A = 1/2 * b * h, where b is the length of the base and h is the height of the triangle.

Since triangle BCD is a right isosceles triangle, we know that the base and height are equal. Let's call this length x. Now, to find x, we can use the Pythagorean Theorem.

In triangle ADC, we know that the length of the hypotenuse is 3 - sqrt(3), the length of one leg is x, and the length of the other leg is x * sqrt(3). Using the Pythagorean Theorem, we can set up the equation:

(3 - sqrt(3))^2 = x^2 + (x * sqrt(3))^2

Simplifying this, we get:

9 - 6sqrt(3) + 3 = 4x^2

or

4x^2 = 12 - 6sqrt(3)

Dividing both sides by 4, we get:

x^2 = 3 - (3/2)sqrt(3)

Taking the square root of both sides, we get:

x = sqrt(3 - (3/2)sqrt(3))

Now, we can plug this value of x into our formula for the area of triangle BCD:

A = 1/2 * x * x

= 1/2 * (3 - (3/2)sqrt(3))

= 3/4 - (3/4)sqrt(3)

So, the area of triangle BCD is 3/4 - (3/4)sqrt(3). I hope this helps and good luck with the rest of your problem!