- #1
AAli
- 3
- 0
Hi I'm having a slight issue trying to obtain a 2nd order ODE with respect to x (so involves implicit differentiation in this case) from the equation below. I would greatly appreciate any help or tips to solve this problem.
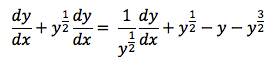
I've removed the coefficients to make things a litter easier. Thank you.
I've removed the coefficients to make things a litter easier. Thank you.
Attachments
Last edited by a moderator:
 Isn't it just dy/dx = - y. ?
Isn't it just dy/dx = - y. ?