Two DOF Anglepoise Spring-balance with Distributed weight

[kavaro]

I am designing a a robot arm based on the two degree of freedom anglepoise lamp, like the typical desk lamp or Pixar lamp, that consists of two parallelograms, each balanced with a spring. The goal is to design it so that it remains statically balanced at all positions and let two springs carry all the weight of the payload. This will drastically reduce the torque requirements of the motors and therefore make it cheaper. The additional benefit is that, because of the parallelograms, the payload does not tilt as the structure is moved.

I'm working from this article:
http://eprints.lancs.ac.uk/20295/1/20295.pdf
The spring-and-lever balancing mechanism, George Carwardine and the Anglepoise Lamp
M J French and M B Widden
Engineering Department, Faculty of Applied Sciences, Lancaster University, UK

The article very clearly describes how to calculate the required spring constants (for the required zero free length springs) for models in which the mass of the structure of the arm is negligible (k = mgr/bc).

For including the mass, the article only explains the process for the 'more elegant' two DOF model in which all the springs are at the base of the structure.

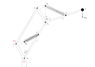
I am now trying to calculate the spring constants for the two DOF structure with the parallelograms by incorporating the mass of the structure itself. If you look at the attached pictures, you can see that the problem is easy if P1 and P2 are in a vertical line, because the center of mass of each link of the structure can be measured from the the same reference.

My problem is that I can't seem to find a solution that incorporates the mass of the structure and is balanced for all angles when P1 and P2 is not in a vertical line.

Any help would be greatly appreciated.

 

[Baluncore]

Only if you use the linkage shown in Fig.4. of your reference, is there a simple solution involving the mass of the links.