Emmanuel_Euler
- 142
- 11
what is the derivative of x! ??
The discussion revolves around the derivative of the factorial function, denoted as x!, and its relationship with the Gamma function. Participants explore the definitions, continuity, and differentiability of these functions, as well as various mathematical properties and approximations related to them.
There is no consensus on the existence of the derivative of x! or the definitions and properties of the Gamma function. Multiple competing views remain regarding the continuity and differentiability of these functions, as well as their definitions and relationships.
Participants highlight limitations in definitions and continuity, particularly regarding the Gamma function's behavior at negative integers and the interpretation of factorials for non-integer values.
pwsnafu said:but x! is only defined on the natural numbers
This is not correct...daverusin said:The previous response is quite correct
certainly said:In-fact the value of the gamma function can also be computed for all negative integers
But I believe it is not continuous in ##\mathbb {R}^-##.
certainly said:This is not correct...
The gamma function is defined for all ##x## and values of the function can be found for infinitely many rational arguments by the identity ##\Gamma(\frac{1}{2})=\sqrt{\pi}##
Also note that this means that ##\Big(-\frac{1}{2}\Big)!=\sqrt{\pi}##. Values of the function exist for other rational numbers as well but they are somewhat complicated.
Also the gamma function is continuous in the domain ##\mathbb{R}^+##
See this stackexchange thread......
Sorry....that was a silly error on my part.....micromass said:It is. It is meromorphic, which means that it induces a continuous (even holomorphic) function ##\Gamma:\mathbb{C}\rightarrow \mathbb{C}_\infty##, where ##\mathbb{C}_\infty## is the Riemann sphere.
Perhaps I should have been a little more careful.micromass said:The gamma function has poles at the negative integers. It is not defined there. And if it were to be defined, it would be ∞\infty (in the one-point compactification of C\mathbb{C}).
While teaching this approach is more intuitive and often historically accurate, however, in practice, the general version (what maybe called the extended version) is always preferred as a definition. So perhaps my reply should have been something like, now that you know about the gamma function the answer will be the derivative of the gamma function......pwsnafu said:If you define the factorial as the gamma sure. Most texts don't. They define the factorial as a product, and show that the gamma function is an extension of the factorial.
certainly said:[It's sort of like an extended gamma function, obtained by defining the gamma function in terms of a "neutrix".]
do the exponent short cut or you can find the limit of the function as Δx→0.Emmanuel_Euler said:Thanks to all who helped me.
but please can you give me the derivative formula??
You can not say that the gamma function and factorial are the same function. They are not defined on the same domain or in the same way. Just because gamma is an extension of factorial does not mean that factorial is more than its original, simple definition.certainly said:This is not correct...
The gamma function is defined for all ##x## .
Still, think of the differential quotient. If x! is defined only on the integers, what is then ##f(x+h) , h \rightarrow 0## ?Emmanuel_Euler said:what is the derivative of x! ??
daverusin said:It's also worth learning Stirling's Approximation: x! is roughly (x/e)^x sqrt(2 pi x ) . That's a formula you can differentiate using calculus-1 tools.
Friend it is not that easy to solve.lonely_nucleus said:do the exponent short cut or you can find the limit of the function as Δx→0.
da/dh=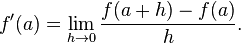
Does the wolfram alpha show the steps??phion said:Wolfram Alpha states the derivative of x! is \Gamma (x+1) \psi^{0}(x+1).
I was hoping it would, but it does not.Emmanuel_Euler said:Does the wolfram alpha show the steps??
It usually does, but i do not think that it will show me the steps only the formula.
Again i want to thank you all.
Oh really?WWGD said:I think Wolfram is computing the derivative of the Gamma function, not of x!
phion said:Oh really?
We're reduced to finding the factorial of a fraction with the gamma function I think.WWGD said:Well, if this is the standard derivative of x!, defined for integers, what is then ##f(a+h):=(a+h)!## , for ## 0<h<1 ## ?
But then, like it has been posted, it is not the ##x!## function.phion said:We're reduced to finding the factorial of a fraction with the gamma function I think.
I still don't see how what Wolfram Alpha stated was actually the derivative of the gamma function.WWGD said:But then, like it has been posted, it is not the #x!# function.
Got it.pwsnafu said:The digamma is the logarithmic derivative of the gamma. If you multiply by the gamma what do you get?