- #1
Miike012
- 1,009
- 0
Please look at the picture...
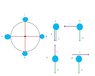
It is of a blue object in four locations that is swung around with a rope ( red line ) in a circle with constant velocity...
I wanted to know if my diagrams are correct for each separate location... and I was hoping someone could check my work below to tell me if it is correct...
1. ƩFx = 0; ƩFy = -T - W = (m)(a) and T = W
2. ƩFx = -T - W = (m)(a) ƩFy = 0 and T> W
3. ƩFx = 0; ƩFy = +T - W = (m)(a) and T>W
4. ƩFx = T - W = (m)(a) ƩFy = 0 and T>W
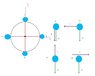
It is of a blue object in four locations that is swung around with a rope ( red line ) in a circle with constant velocity...
I wanted to know if my diagrams are correct for each separate location... and I was hoping someone could check my work below to tell me if it is correct...
1. ƩFx = 0; ƩFy = -T - W = (m)(a) and T = W
2. ƩFx = -T - W = (m)(a) ƩFy = 0 and T> W
3. ƩFx = 0; ƩFy = +T - W = (m)(a) and T>W
4. ƩFx = T - W = (m)(a) ƩFy = 0 and T>W