Is the Left Angle of the CKM Unitarity Triangle Really Pi Minus Gamma?

[Valeriia Lukashenko]

Homework Statement

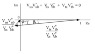
I want to proof for $$V_{us}V^{*}_{ub}+V_{cs}V^{*}_{cb}+V_{ts}V^{*}_{tb}=0$$ unitarity triangle that left angle is $$\pi-\gamma$$ (see below picture from my lecture notes).

Homework Equations

[/B]
$$\gamma \approx - arg(V_{ub})$$
$$\beta_s \approx arg(V_{ts})+\pi$$
$$arg(V_{us}V_{ub}^{*})=arg(V_{ub}^{*})$$
since only V_ub^*has an imaginry part on this order of Wolfstein parametrization.
$$arg(V_{ts}V_{tb}^{*})=arg(V_{ts})$$
same reason

V_cs and V_cb^* are real.

The Attempt at a Solution

Let's call the angle we want to know δ.

$$\delta=\pi+arg(V_{us}V_{ub}^{*})-arg(V_{ts}V_{tb}^{*})=\pi+arg(V_{ub}^{*})-arg(V_{ts})=\pi - arg(V_{ub})+\pi - \beta_s =2\pi -(\beta_s+arg(V_{ub}))=-(\beta_s-\gamma)=\gamma-\beta_s$$

and it is not equal to π-γ.
Could anyone, please, check my solution, because I don't get where my mistake is.

 

[Orodruin]

Homework Statement

I want to proof for $$V_{us}V^{*}_{ub}+V_{cs}V^{*}_{cb}+V_{ts}V^{*}_{tb}=0$$ unitarity triangle that left angle is $$\pi-\gamma$$ (see below picture from my lecture notes).

What do you mean by "proof for"? If you assume unitarity of the CKM matrix, it follows directly from one of the elements of the unitarity condition $V^\dagger V = 1$. If you want to have an experimental confirmation of this you need to measure each of the elements. If you want to know why those numbers form a triangle in the complex plane, it is a simple matter of addition of complex numbers.

 

[Valeriia Lukashenko]

What do you mean by "proof for"? If you assume unitarity of the CKM matrix, it follows directly from one of the elements of the unitarity condition $V^\dagger V = 1$. If you want to have an experimental confirmation of this you need to measure each of the elements. If you want to know why those numbers form a triangle in the complex plane, it is a simple matter of addition of complex numbers.

Yeah, I guess I was not clear in my question. So, $\gamma$ is defined using "The" unitarity triangle ($V_{ud}V_{ub}^{*}+V_{cd}V_{cb}^{*}+V_{td}V_{tb}^{*}=0$). In the triangle above $\gamma$ appears again. In the picture, it appears in left angle $\pi - \gamma$. I tried to check if this is correct and it didn't work. The result that I get is $\gamma-\beta_s$ for the same angle. I couldn't find any references to cross-check the above triangle (usually one draws "The" unitarity triangle and very schematically other without indicating angles). And I am trying to get is it my lack of understanding of how to properly build/work with unitarity triangle, so I don't get the right answer or my answer is correct and there is a mistake in lecture notes.