MHB Unknown_12's questions at Yahoo Answers regarding analytic geometry

[MarkFL]

Here are the questions:

Question on analytic geometry about slopes?


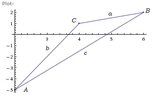
Find the interior angle of the triangle with vertices (2, -5), (6,2), (4,1)

It must 180 degrees when calculated but stuck on the solution.

The line through (-2, y) and (2, 10) is perpendicular to a line through (-3, -7) and (5, -5) find y.

The formula will be like y2-y1 / x2- x1

and formula for angle tan m2-m1/1+m1(m2)

solution of the answer is appreciated.

I have posted a link there to this thread so the OP can see my work.

 

[MarkFL]

Hello unknown_12,

1.) Let's take a look at the triangle in the plane with the given vertices:

https://www.physicsforums.com/attachments/1709._xfImport

The slope of line segment $a$ is:

$$m_a=\frac{2-1}{6-4}=\frac{1}{2}$$

The slope of line segment $b$ is:

$$m_b=\frac{1-(-5)}{4-2}=3$$

The slope of line segment $c$ is:

$$m_c=\frac{2-(-5)}{6-2}=\frac{7}{4}$$

Hence, angle $A$ is:

$$A=\tan^{-1}\left(m_b \right)-\tan^{-1}\left(m_c \right)=\tan^{-1}\left(3 \right)-\tan^{-1}\left(\frac{7}{4} \right)\approx0.197395559849881$$

Angle $B$ is:

$$B=\tan^{-1}\left(m_c \right)-\tan^{-1}\left(m_a \right)=\tan^{-1}\left(\frac{7}{4} \right)-\tan^{-1}\left(\frac{1}{2} \right)\approx0.588002603547568$$

Angle $C$ is:

$$C=\pi-\left(\tan^{-1}\left(m_b \right)-\tan^{-1}\left(m_a \right) \right)=\pi+\tan^{-1}\left(\frac{1}{2} \right)-\tan^{-1}(3)=\frac{3\pi}{4}$$

As a check, we see that:

$$A+B+C=\pi$$

2.) The slope of the first line is:

$$m_1=\frac{10-y}{2-(-2)}=\frac{10-y}{4}$$

The slope of the second line is:

$$m_2=\frac{-5-(-7)}{5-(-3)}=\frac{1}{4}$$

When two lines are perpendicular, the product of their slopes is $-1$, as proven here:

http://mathhelpboards.com/math-notes-49/perpendicular-lines-product-their-slopes-2953.html

Hence, we must have:

$$\frac{10-y}{4}\cdot\frac{1}{4}=-1$$

$$10-y=-16$$

$$y=26$$

 

[jamescv31]

Hello, I'm the one posted from yahoo answer; is that same from the tangent formula that I've posted?

Because when I used the formula, it couldn't provide a 180 degrees.

 

[MarkFL]

Hello, I'm the one posted from yahoo answer; is that same from the tangent formula that I've posted?

Hello and welcome to MHB, jamescv31! :D

I take it you are supposed to use the angle-difference identity for the tangent function instead of the product of the slopes.

$$\theta_1-\theta_2=\frac{\pi}{2}$$

Taking the tangent of both sides, we get:

$$\tan\left(\theta_1-\theta_2 \right)=\tan\left(\frac{\pi}{2} \right)$$

$$\frac{m_1-m_2}{1+m_1m_2}=\tan\left(\frac{\pi}{2} \right)$$

Since $$\tan\left(\frac{\pi}{2} \right)$$ is undefined, we see that we require:

$$1+m_1m_2=0$$

$$m_1m_2=-1$$

 

[MarkFL]

...Because when I used the formula, it couldn't provide a 180 degrees.

This was added while I was composing my reply. I assume this refers to the first problem. You want the sum of the 3 angles to be $180^{\circ}=\pi$.

Do you understand how I computed the values of the individual angles?

 

[jamescv31]

Yes I'm referring on the interior problem, since our teacher provided this formula only for the discussion

the Tangent = m2+m1/ 1 + m1m2

Which the goal is to have an equal 180 degrees or 179.9 as possible.

 

[jamescv31]

Could I manage to have an exact 180 degrees with the formula of tangent
m2-m1/1+m1m2 ?

- - - Updated - - -

Well nevermind, got already.

Thank you for the time. :)

 

[MarkFL]

Yes I'm referring on the interior problem, since our teacher provided this formula only for the discussion

the Tangent = m2+m1/ 1 + m1m2

Which the goal is to have an equal 180 degrees or 179.9 as possible.

Okay, well using the formula you originally gave, we find:

$$A=\tan^{-1}\left(\frac{m_b-m_c}{1+m_am_b} \right)=\tan^{-1}\left(\frac{3-\frac{7}{4}}{1+3\cdot\frac{7}{4}} \right)=\tan^{-1}\left(\frac{1}{5} \right)\approx0.197395559849881$$

$$B=\tan^{-1}\left(\frac{m_c-m_a}{1+m_am_c} \right)=\tan^{-1}\left(\frac{\frac{1}{2}-\frac{7}{4}}{1+\frac{1}{2}\cdot\frac{7}{4}} \right)=\tan^{-1}\left(\frac{2}{3} \right)\approx0.588002603547568$$

$$C=\pi+\tan^{-1}\left(\frac{m_a-m_b}{1+m_am_b} \right)=\pi+\tan^{-1}\left(\frac{\frac{1}{2}-3}{1+\frac{1}{2}\cdot3} \right)=\pi+\tan^{-1}\left(-1 \right)=\pi-\frac{\pi}{4}=\frac{3\pi}{4}$$

Note: For angle $C$ it was necessary to add $\pi$ to get the angle in the correct quadrant.

If we convert the angles to degrees, we find:

$$A\approx11.31^{\circ}$$

$$B\approx33.69^{\circ}$$

$$C=135^{\circ}$$

We see then that:

$$A+B+C\approx180^{\circ}$$