Usage of First Order Elastic Constants in Soft Body Equations

[doenn1616]

TL;DR Summary

Trying to properly index elastic constants in elasticity equations.

Hi, I have some soft body equations that require first order elasticity constants. Just trying to figure out the proper indexing.

From Finite Elements of Nonlinear Continua by J.T. Oden, the elastic constants I am trying to obtain are the first order, circled below:

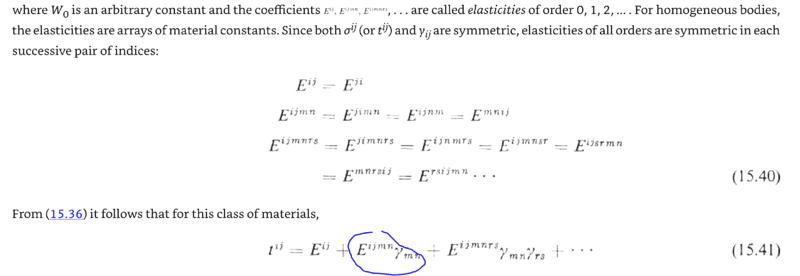
My particular constitutive equation doesn't need the zeroeth order, just first (circled in blue) or higher. I have a quite lengthy tutorial from Nasa on elastic constants called An In-Depth Tutorial on Constitutive Equations for Elastic Anisotropic Materials by Michael Nemeth, which includes:

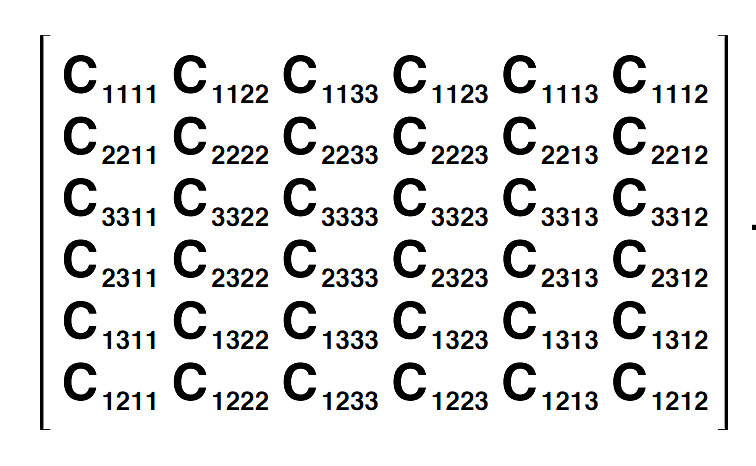
So, say I need the constant at index 2,1,3,2. I see that in the full matrix only, circled below in blue:

I see there is symmetry, but can't figure out yet how to get this one. From the Materials Project Database, I have some elasticities of a material
Nb4CoSi:

"elastic_tensor": [
[
311.33514638650246,
144.45092552856926,
126.17558149507941,
0.0,
-0.11034746666666635,
0.0
],
[
144.45092552856926,
311.3204320131957,
126.16885826858503,
0.0,
-0.11216067833333321,
0.0
],
[
126.17558149507941,
126.16885826858503,
332.18500448217554,
0.0,
-0.10754095333333334,
0.0
],
[
0.0,
0.0,
0.0,
98.91818763333335,
0.0,
0.0
],
[
-0.11034746666666635,
-0.11216067833333321,
-0.10754095333333334,
0.0,
98.92097952333339,
0.0
],
[
0.0,
0.0,
0.0,
0.0,
0.0,
103.33913232000003
]
],

Which is only a 6x6 matrix. Is there something simple I can do to use these constants? Am I confined to a lower order? Confusing since Eijmn looks fourth order when Oden says first. Am I close or is there a lot more to do?

Regards.

 

[pasmith]

In view of the symmetry relations $C_{2132} = C_{1223}$. Since $\sigma_{ij}$ and $\epsilon_{ij}$ are symmetric they each have only six independent entries, which can be related to each other by a 6x6 matrix.

 

[robphy]

Confusing since Eijmn looks fourth order when Oden says first.

Distinguish
“first order” as “one factor of $\gamma$ in the expansion” (“linear in $\gamma$”)
from
“fourth order” or “fourth rank” as “four indices” in that $E$-tensor (as a multilinear mapping of four vectors to the reals).

 

[doenn1616]

Yeah, yeah, you're totally right.. where is my mind at!

So,

C2132 = C1232 = C1223 and Eijmn also equals Ejinm.

Since Ejinm wasn't specified, just wanted to double check. And sorry for the delay, want to be thorough in proving these symmetries check out, but my mind is super full trying to simulate this and some fluid equations graphically, kind of digesting this slow this week. Take care..!