- #1
Vadar2012
- 208
- 2
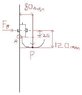
I'm going to bolt some hooks to the inside walls of 20ft and 40ft shipping containers. What I'm wondering is, what would be the easiest way to determine the stress on the corrugated steel walls, excerted on it by placing things on these hooks?. The hooks are 280mm apart and the force will be applied at approx 80mm from the wall. The steel is 14 gauge (2mm thick) and has a yield strength of 350 MPa.
So far I've done an FEA model in strand7. I drew the profile of the corrugated sheet using plates and then simulated the hooks by creating nodes at the approx position of the weight and used a rigid link to tie it to the plates. This gives a max stress much higher than I anticipated. Restraints are all ends fixed.
Anyone got any better ideas on how to better apply the load from the hooks? Or would it just be better to just approximate it as a simple flat plate? How would you determine the uniform load per unit area for this case?
Any other ideas on how best to determine this?
All help is appreciated.
So far I've done an FEA model in strand7. I drew the profile of the corrugated sheet using plates and then simulated the hooks by creating nodes at the approx position of the weight and used a rigid link to tie it to the plates. This gives a max stress much higher than I anticipated. Restraints are all ends fixed.
Anyone got any better ideas on how to better apply the load from the hooks? Or would it just be better to just approximate it as a simple flat plate? How would you determine the uniform load per unit area for this case?
Any other ideas on how best to determine this?
All help is appreciated.