What else could we do? (p-adic expansion)

[evinda]

Hello! (Wave)

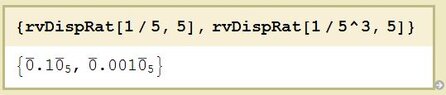
I want to find the p-adic expansion of $\frac{1}{p}$ and $\frac{1}{p^r}$ in the field $\mathbb{Q}_p$.

So, do I have to solve the congruences $px \equiv 1 \pmod {p^n}, p^r x \equiv 1 \pmod { p^n }, \forall n \in \mathbb{N} $, respectively?

But.. these congruences do not have solutions, right? (Thinking)

What else could we do, in order to find the p-adic expansion of $\frac{1}{p}$ and $\frac{1}{p^r}$ in $\mathbb{Q}_p$ ? (Worried)

 

[RLBrown]

If you are trying to express 1/p and 1/p^r as a list of p-adic integer digits,
{a₀, a₁, a₂, ... }
then it is correct " these congruences do not have solutions"

These are not p-adic integers. The digit list has non-zero a_n, for n<0.

Case 1/p:
all digits zero except a_-1 = 1

Case 1/p^r:
all digits zero except a_-r = 1

Examples: 1/5 and 1/5^3 as 5-adic
View attachment 3455
Conventions as in this DEMO