Capde10
- 1
- 0
What is "linear acceleration" in uniform circular motion?
Yesterday, I took an exam and it was asked a concept that we hadn't studied, at least in the way it was written.
The exercise explained that a circular motion was decreasing its velocity, and we had to be able to identify which of the following diagrams represent linear velocity (no problem, I can identify and calculate it) as well as linear acceleration (problem, a concept that I can't find anywhere, either on Internet)
These were the 3 diagrams:
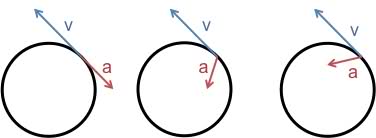
I chose the first one because I thought (as well as most of my classmates) that as the acceleration is linear, it must be tangent to the trajectory, as with linear velocity. Moreover, it must have the opposite direction because the velocity is decreasing so acceleration is negative. However, according to my teacher, the correct one is the third one, because linear acceleration always goes to the center of the tragectory.
Which is the correct one?
Thanks.
Yesterday, I took an exam and it was asked a concept that we hadn't studied, at least in the way it was written.
The exercise explained that a circular motion was decreasing its velocity, and we had to be able to identify which of the following diagrams represent linear velocity (no problem, I can identify and calculate it) as well as linear acceleration (problem, a concept that I can't find anywhere, either on Internet)
These were the 3 diagrams:
I chose the first one because I thought (as well as most of my classmates) that as the acceleration is linear, it must be tangent to the trajectory, as with linear velocity. Moreover, it must have the opposite direction because the velocity is decreasing so acceleration is negative. However, according to my teacher, the correct one is the third one, because linear acceleration always goes to the center of the tragectory.
Which is the correct one?
Thanks.