What is the area of this parallelogram?

[eXoo]

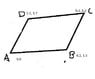
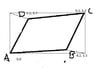
1. I'll illustrate the question, I've been having a lot of troubles with it, the image is in the attachements.

2. I've tried it many times, with different methods but keep getting different answers. Really need help with it. Most recently tried by splitting it into two triangles then working out from there, got 12.86, but it's most likely wrong.

Thanks :)

 

[genericusrnme]

if you know about determinants then take the determinant of the matrix with the vectors AB and BL in it's rows

other wise, try constructing a rectangle of length 5.3 and height 5.2 and take some squared and triangles away

ask again if you need another hint

 

[eXoo]

if you know about determinants then take the determinant of the matrix with the vectors AB and BL in it's rows

other wise, try constructing a rectangle of length 5.3 and height 5.2 and take some squared and triangles away

ask again if you need another hint

My teacher has taught us neither of those ways, so I don't really know how to get a result with them. :(

 

[genericusrnme]

if you can calculate the area of a triangle and a rectangle you'll be able to find the area by constructing a rectangle and cutting parts out of it

if you set it up and play about for a bit you should be able to see what parts to cut out and from then on it's pretty basic calculations

 

[eXoo]

if you can calculate the area of a triangle and a rectangle you'll be able to find the area by constructing a rectangle and cutting parts out of it

if you set it up and play about for a bit you should be able to see what parts to cut out and from then on it's pretty basic calculations

still don't get it :(

 

[gneill]

If you draw a diagonal you have two similar triangles. Further, you can find the lengths of all the sides of the triangles.

What methods do you know for finding the area of a triangle from its side lengths? Have you heard of Heron's Formula? (You should have come across it in high school math)

You can also solve the problem using vectors: The cross product of two (non parallel) vectors in a plane yields a vector whose magnitude is the area of the parallelogram with those vectors forming two of its sides.

 

[genericusrnme]

Look at my attachment, hopefully that should help
calculate the area of the square and take away parts to find the area of your parallelogram

 

[eumyang]

I think this is what genericusrnme was getting at. The attachment shows the parallelogram enclosed inside a rectangle. Find the area of the rectangle, and then subtract the areas of the four triangles, and you'll get the area of the parallelogram.EDIT: Beaten to it.