SUMMARY
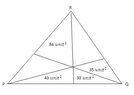
Triangle PQR is divided into six smaller triangles by lines drawn from its vertices through a common interior point. The areas of four of these smaller triangles are provided, allowing for the calculation of the total area of triangle PQR. By applying the principle of area addition and the properties of triangles, the area of triangle PQR can be determined definitively based on the known areas of the smaller triangles.
PREREQUISITES
- Understanding of basic triangle properties
- Knowledge of area calculation methods for triangles
- Familiarity with geometric division of shapes
- Ability to apply algebraic equations to geometric problems
NEXT STEPS
- Study the properties of similar triangles
- Learn techniques for calculating areas of complex geometric shapes
- Explore the concept of centroid and its relation to triangle area
- Investigate geometric transformations and their effects on area
USEFUL FOR
Students studying geometry, educators teaching triangle properties, and anyone interested in solving geometric area problems.